Question

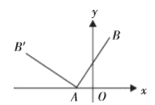
【题目】如图，在平面直角坐标系中，已知，将线段绕着点逆时针旋转90°得到线段，则的坐标为______________

Answer 1

【答案】

【解析】

作BC⊥x轴于C，作B′D⊥x轴，垂足分别为C、D，证明△ABC≌△B′AD，可得AD=BC=3，B′D=AC=2，可得结果．

如图，作BC⊥x轴于C，作B′D⊥x轴，垂足分别为C、D，

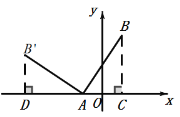
∵点A、B的坐标分别为(-1，0)、(1，3)，
∴AC=1-(-1) =2，BC=3，
∵∠BAB′=90°，
∴∠B′AD+∠BAC=90°，
∵∠BAC+∠ABC=90°，
∴∠ABC =∠B′AD，
∵BA=BA′，∠ACB=∠B′DA，
∴△ABC≌△B′AD，

BC=AD= 3，AC=B′D= 2，
∴OD=AD+AO=3+1=4，
∴点B′的坐标为(，)．
故答案为：(，)．