题目内容
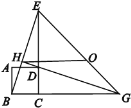
【题目】如图,四边形ABCD是正方形,ΔECG是等腰直角三角形,∠BGE的平分线过点D交BE 于H,O是EG的中点,对于下面四个结论:①GH⊥BE;②OH∥BG,且![]() ;③
;③![]() ;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
A.1B.2C.3D.4
【答案】D
【解析】
①由四边形ABCD是正方形,△ECG是等腰直角三角形,得出△BCE≌△DCG,推出∠BEC+∠HDE=90°,从而得出GH⊥BE;
②由GH是∠EGC的平分线,得出△BGH≌△EGH,再由O是EG的中点,利用中位线定理,得出OH∥BG,且![]() ;
;
③由(2)得BG=EG,设CG=x,则CE=x,根据勾股定理得EG=![]() x,所以BG=
x,所以BG=![]() x,从而得到BC=(
x,从而得到BC=(![]() -1)x,根据正方形面积公式和等腰直角三角形面积公式可以得到S正方形ABCD=(3-2
-1)x,根据正方形面积公式和等腰直角三角形面积公式可以得到S正方形ABCD=(3-2![]() )x2,S△ECG=
)x2,S△ECG=![]() x2,进而求出
x2,进而求出![]() ;
;
④三角形的外接圆的圆心是三条边的垂直平分线的交点,三角形的内切圆是的圆心是三个角的平分线的交点.由(2)得BG=EG,由(1)得GH⊥BE,因为GH平分∠BGE,所以GH是BE边上的垂直平分线,所以△EBG的外接圆圆心和内切圆圆心在直线HG上.
解:①∵四边形ABCD是正方形,△ECG是等腰直角三角形
∴BC=CD,CE=CG,∠BCE=∠DCG=90°
在△BCE和△DCG中,
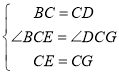
∴△BCE≌△DCG(SAS)
∴∠BEC=∠BGH
∵∠BGH+∠CDG=90°,∠CDG=∠HDE
∴∠BEC+∠HDE=90°
∴GH⊥BE
故①正确;
②∵GH是∠EGC的平分线
∴∠BGH=∠EGH
在△BGH和△EGH中,
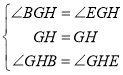
∴△BGH≌△EGH(ASA)
∴BH=EH
∵O是EG的中点
∴HO是△EBG的中位线
∴OH∥BG,且![]()
故②正确;
③由(2)得△BGH≌△EGH
∴BG=EG
在等腰直角三角形ECG中,设CG=x,则CE=x
∴EG=![]() =
=![]() x
x
∴BG=![]() x
x
∴BC=BG-CG=![]() x-x=(
x-x=(![]() -1)x
-1)x
∴S正方形ABCD=BC2=[(![]() -1)x]2 =(3-2
-1)x]2 =(3-2![]() )x2
)x2
S△ECG=![]()
![]() CG
CG![]() CE=
CE=![]() x2
x2
∴S正方形ABCD∶S△ECG=(3-2![]() )x2∶
)x2∶![]() x2=(6-4
x2=(6-4![]() )∶1
)∶1
故③正确;
④由(2)得BG=EG,由(1)得GH⊥BE
∵GH平分∠BGE,
∴GH是BE边上的垂直平分线
∵三角形的外接圆的圆心是三条边的垂直平分线的交点,三角形的内切圆是的圆心是三个角的平分线的交点.
∴△EBG的外接圆圆心和内切圆圆心在直线HG上
故④正确.
故选D.