题目内容
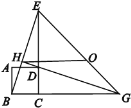
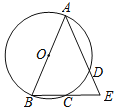
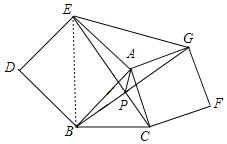
【题目】如图,分别以△ABC的边AB、AC为一边向外做正方形ABDE和正方形ACFG,连结CE、BG交于点P,连结AP和EG.在不添加任何辅助线和字母的前提下,写出四个不同类型的结论_____.

【答案】△AEC≌△ABG,EC=BG,EC⊥BG,AP平分∠EPG,
【解析】
如图,连接BE,由“SAS”可证△EAC≌△BAG,可得EC=BG,∠CEA=∠GBA,可证点P,点A,点E,点B四点共圆,可得∠EPB=∠EAB=90°,∠APE=∠ABE=45°,可得EC⊥BG,AP平分∠EPG.
解:△AEC≌△ABG,EC=BG,EC⊥BG,AP平分∠EPG,(答案不唯一)
理由如下:如图,连接BE,
∵正方形ABDE和正方形ACFG,
∴AB=AE,AC=AG,∠BAE=∠CAG=90°,∠ABE=45°
∴∠EAC=∠BAG,
∴△EAC≌△BAG(SAS),
∴EC=BG,∠CEA=∠GBA,
∵∠CEA=∠GBA,
∴点P,点A,点E,点B四点共圆,
∴∠EPB=∠EAB=90°,∠APE=∠ABE=45°,
∴EC⊥BG,∠EPG=90°,
∴∠APG=∠APE=45°,
∴AP平分∠EPG.

【题目】自从开展“创建全国文明城区“工作以来,门头沟区便掀起了“门头沟热心人“志愿服务的热潮,区教委也号召各校学生积极参与到志愿服务当中.为了解甲、乙两所学校学生一周志愿服务情况,从这两所学校中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)数据进行收集、整理、描述和分析.下面给出了部分信息:
a.甲校40名学生一周的志愿服务时长的扇形统计图如图(数据分成6组:![]() ):
):
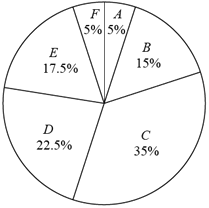
A:![]() B:
B:![]()
C:![]() D:
D:![]()
E:![]() F:
F:![]()
b.甲校40名学生一周志愿服务时长在![]() 这一组的是:
这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 80 80
c.甲、乙两校各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如下:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 75 |
| 90 |
乙校 | 75 | 76 | 85 |
根据以上信息,回答下列问题:
(1)![]() _____________;
_____________;
(2)根据上面的统计结果,你认为____①_____所学校学生志愿服务工作做得好(填“甲“或“乙“),理由______②________________________________________________________;
(3)甲校要求学生一周志愿服务的时长不少于60分钟,如果甲校共有学生800人,请估计甲校学生中一周志愿服务时长符合要求的有_______人.