题目内容
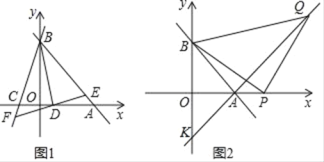
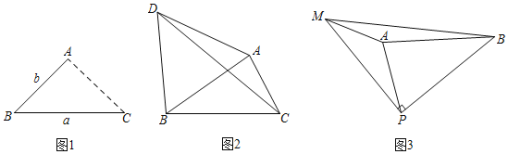
【题目】（1）发现：如图1，点
为线段
外一动点，且
，
，当点位于 时，线段
的长取得最大值，最大值为 （用含
的式子表示）；
（2）应用：如图2，点为线段外一动点，
，
，以
为边作等边
，连接
，求线段的最大值；
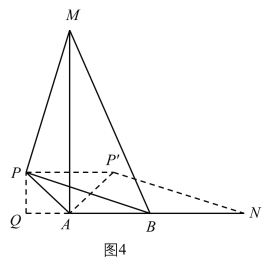
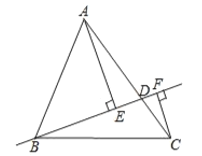
（3）拓展：如图3，线段
，点
为线段外一动点，且
，
，
，求线段
长的最大值及此时
的面积．
【答案】（1）CB的延长线上，a+b；（2）6；（3）最大值为3+
，△PBM的面积为
【解析】
（1）根据点A位于CB的延长线上时，线段AC的长取得最大值，即可得到结论；
（2）根据等边三角形的性质得到AD=AB，AC=AE，∠BAD=∠CAE=60°，推出△CAD≌△EAB，根据全等三角形的性质得到CD=BE，利用（1）中的结论即可得到结果；
（3）将△APM绕着点P顺时针旋转90°得到△AP'N，连接BN，得到△APP'是等腰直角三角形，根据全等三角形的性质得到P'A=PA=2，AN=AM，根据当N在线段BA的延长线时，线段BN取得最大值，即可得到最大值为+3，过点P作PQ⊥AB的延长线于点Q，
利用勾股定理求出PB的长，根据△PBM为等腰直角三角形，可求出面积.
解：（1）∵点A为线段BC外一动点，且BC=a，AB=b，
∴当点A位于CB的延长线上时，线段AC的长取得最大值，且最大值为BC+AB=a+b，
故答案为：CB的延长线上，a+b；
（2）如图2中，以AC为边向上作等边△ACE，连接BE．
∵△ABD与△ACE是等边三角形，
∴AD=AB，AC=AE，∠BAD=∠CAE=60°，
∴∠BAD+∠BAC=∠CAE+∠BAC，
即∠CAD=∠EAB，
在△CAD与△EAB中，
，
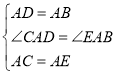∴△CAD≌△EAB（SAS），
∴CD=BE；
∴线段BE长的最大值=线段CD的最大值，
∴由（1）知，当线段BE的长取得最大值时，点E在BA的延长线上，
∴最大值为=4+2=6．
∴线段CD的最大值为6；
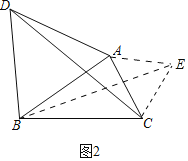
（3）解：如图3中，将△APM绕着点A顺时针旋转90°得到△AP'N，连接BN，PP′．
∴△APM≌△AP'N，
∴AN=AM，AP=AP'=2，
∴线段AM长的最大值=线段AN长的最大值，
∴当N在线段AB的延长线时，线段AN取得最大值，最大值=AB+BN，
∴∠PAP'=90°，
∴△APP'是等腰三角形，
∴PP'=，
∵△BPM是等腰直角三角形，
∴∠BPM=∠MAN=90°，PM=PB=P'N，
∴∠AMP=∠ABP=∠N，
∴PB∥P'N，
∴四边形PBNP'是平行四边形，
∴BN=PP'，
∴AN的最大值为：AB+BN=AB+PP'=3+，
∴AM的最大值为3+，
过点P作PQ⊥AB的延长线于点Q，
∵∠PAP′=90°，∠P′AB=∠PP′A=45°，
∴∠PAQ=45°，
∴△PAQ为等腰直角三角形，
∵AP=2，由勾股定理可得：
∴AQ=PQ=
，
在△PBQ中，PQ2+BQ2=PB2，
即
，
∴PB2=
，
∵△PBM为等腰直角三角形，
此时△PBM的面积=
×=.
