ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЃЌжБЯпyЃНЉx+bЗжБ№гыxжсЃЌyжсНЛгкAЃЈ6ЃЌ0ЃЉЃЌBСНЕуЃЌЙ§ЕуBЕФСэвЛжБЯпНЛxжсЕФИКАыжсгкЕуCЃЌЧвOBЃКOCЃН3ЃК1
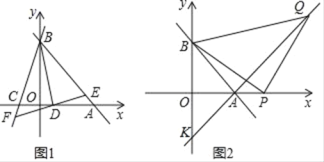
ЃЈ1ЃЉЧѓжБЯпBCЕФНтЮіЪНЃЛ
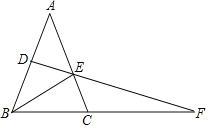
ЃЈ2ЃЉжБЯпyЃНaxЉaЃЈaЁй0ЃЉНЛABгкЕуEЃЌНЛBCгкЕуFЃЌНЛxжсгкЕуDЃЌЪЧЗёДцдкетбљЕФжБЯпEFЃЌЪЙSЁїBDEЃНSЁїBDFЃПШєДцдкЃЌЧѓГіaЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
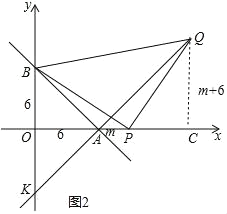
ЃЈ3ЃЉШчЭМ2ЃЌЕуPЮЊAЕугвВрxжсЩЯвЛЖЏЕуЃЌвдPЮЊжБНЧЖЅЕуЃЌBPЮЊбќдкЕквЛЯѓЯоФкзїЕШбќжБНЧШ§НЧаЮЁїBPQЃЌСЌНгQAВЂбгГЄНЛyжсгкЕуKЃЎЕБPЕудЫЖЏЪБЃЌKЕуЕФЮЛжУЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓГіЫќЕФзјБъЃЛШчЙћЛсЗЂЩњБфЛЏЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН3x+6ЃЛЃЈ2ЃЉДцдкЃЌaЃН![]() ЃЛЃЈ3ЃЉKЕуЕФЮЛжУВЛЗЂЩњБфЛЏЃЌKЃЈ0ЃЌЉ6ЃЉ
ЃЛЃЈ3ЃЉKЕуЕФЮЛжУВЛЗЂЩњБфЛЏЃЌKЃЈ0ЃЌЉ6ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШШЗЖЈBЁЂCСНЕузјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉгЩSЁїBDFЃНSЁїBDEПЩжЊжЛашDFЃНDEЃЌМДDЮЊEFжаЕуЃЌСЊСЂНтЮіЪНЧѓГіEЁЂFСНЕузјБъЃЌРћгУжаЕузјБъЙЋЪНСаГіЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЙ§ЕуQзїQCЁЭxжсЃЌжЄУїЁїBOPЁеЁїPCQЃЌЧѓГіACЃНQCЃЌМДПЩЭЦГіЁЯQACЃНЁЯOAKЃН45ЁуЃЌМДПЩНтОіЮЪЬт.
НтЃКЃЈ1ЃЉЁпжБЯпyЃНЉx+bгыxжсНЛгкAЃЈ6ЃЌ0ЃЉЃЌ
Ёр0ЃНЉ6+bЃЌНтЕУЃКbЃН6ЃЌ
ЁржБЯпABЕФНтЮіЪНЪЧЃКyЃНЉx+6ЃЌ
ЁрBЃЈ0ЃЌ6ЃЉЃЌ
ЁрOBЃН6ЃЌ
ЁпOBЃКOCЃН3ЃК1ЃЌ
ЁрOCЃН2ЃЌ
ЁрCЃЈЉ2ЃЌ0ЃЉ
ЩшжБЯпBCЕФНтЮіЪНЪЧyЃНkx+bЃЌ
Ёр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпBCЕФНтЮіЪНЪЧЃКyЃН3x+6ЃЛ
ЃЈ2ЃЉДцдкЃЎ
РэгЩЃК ЁпSЁїBDFЃНSЁїBDEЃЌ
ЁржЛашDFЃНDEЃЌМДDЮЊEFжаЕуЃЌ
ЁпЕуEЮЊжБЯпABгыEFЕФНЛЕуЃЌ
СЊСЂ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК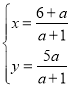 ЃЌ
ЃЌ
ЁрЕуEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпЕуFЮЊжБЯпBCгыEFЕФНЛЕуЃЌ
СЊСЂ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК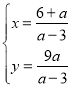 ЃЌ
ЃЌ
ЁрЕуFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁпDЮЊEFжаЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрaЃН0ЃЈЩсШЅЃЉЃЌaЃН![]() ЃЌ
ЃЌ
ОМьбщЃЌaЃН![]() ЪЧдЗНГЬЕФНтЃЌ
ЪЧдЗНГЬЕФНтЃЌ
ЁрДцдкетбљЕФжБЯпEFЃЌaЕФжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉKЕуЕФЮЛжУВЛЗЂЩњБфЛЏЃЎ
РэгЩЃКШчЭМ2жаЃЌЙ§ЕуQзїQCЁЭxжсЃЌЩшPAЃНmЃЌ
ЁпЁЯPOBЃНЁЯPCQЃНЁЯBPQЃН90ЁуЃЌ
ЁрЁЯOPB+ЁЯQPCЃН90ЁуЃЌЁЯQPC+ЁЯPQCЃН90ЁуЃЌ
ЁрЁЯOPBЃНЁЯPQCЃЌ
ЁпPBЃНPQЃЌ
ЁрЁїBOPЁеЁїPCQЃЈAASЃЉЃЌ
ЁрBOЃНPCЃН6ЃЌOPЃНCQЃН6+mЃЌ
ЁрACЃНQCЃН6+mЃЌ
ЁрЁЯQACЃНЁЯOAKЃН45ЁуЃЌ
ЁрOAЃНOKЃН6ЃЌ
ЁрKЃЈ0ЃЌЉ6ЃЉЃЎ