题目内容
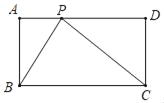
【题目】如图,在长方形ABCD中,AB=2,BC=4,点P在AD上,若△PBC为直角三角形,则CP的长为_____.
【答案】2![]() 或2
或2![]() 或2
或2
【解析】
分情况讨论:①当∠PBC=90°时,P与A重合,由勾股定理得CP=![]() ;②当∠BPC=90°时,由勾股定理得22+AP2+22+(4﹣AP)2=16,求出AP=2,DP=2,由勾股定理得出CP=
;②当∠BPC=90°时,由勾股定理得22+AP2+22+(4﹣AP)2=16,求出AP=2,DP=2,由勾股定理得出CP=![]() ;③当∠BCP=90°时,P与D重合,CP=CD=2.
;③当∠BCP=90°时,P与D重合,CP=CD=2.
解:∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=4,∠A=∠ABC=∠BCD=∠D=90°,
分情况讨论:①当∠PBC=90°时,P与A重合,
由勾股定理得:CP=![]() ;
;
②当∠BPC=90°时,
由勾股定理得:BP2=AB2+AP2=22+AP2,CP2=CD2+DP2=22+(4﹣AP)2,BC2=BP2+CP2=42,
∴22+AP2+22+(4﹣AP)2=16,
解得:AP=2,
∴DP=2,
∴CP=![]() ;
;
③当∠BCP=90°时,P与D重合,CP=CD=2;
综上所述,若△PBC为直角三角形,则CP的长为![]() 或
或![]() 或2;
或2;
故答案为:2![]() 或2
或2![]() 或2.
或2.

练习册系列答案
相关题目