题目内容
【题目】已知线段AB=60cm.
![]()
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,同时点Q沿线段BA自B点 向A点以4厘米/秒运动,问经过几秒后P、Q相遇?
(2)在(1)的条件下,几秒钟后,P、Q相距12cm?
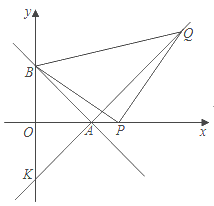
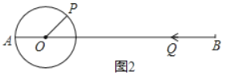
(3)如图2,AO=PO=10厘米,∠POB=40°,点P绕着点O以10度/秒的速度顺时针 旋转一周停止,同时点Q沿线段BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
【答案】(1) 经过10秒钟后P、Q相遇;(2) 经过8秒钟或12秒钟后,P、Q相距12cm;(3) 点Q运动的速度为10cm/s或![]() cm/s.
cm/s.
【解析】
(1)根据相遇问题中的等量关系列方程求解即可;
(2)分相遇前相距12cm和相遇后相距12cm,分别列方程求解即可;
(3)由于点P,Q只能在直线AB上相遇,所以可先求出点P两次旋转到直线AB上的时间,然后分别列出方程求解即可.
解:(1)设经过t秒后P、Q相遇,
由题意得:2t+4t=60,
解得t=10,
答:经过10秒钟后P、Q相遇;
(2)设经过x秒P、Q相距12cm,
当相遇前相距12cm时,
由题意得:2x+4x+12=60,
解得:x=8,
当相遇后相距12cm时,
由题意得:2x+4x-12=60,
解得:x=12,
答:经过8秒钟或12秒钟后,P、Q相距12cm;
(3)设点Q运动的速度为ycm/s,
∵点P,Q只能在直线AB上相遇,
∴点P第一次旋转到直线AB上的时间为:40÷10=4s,
若此时相遇,则4y=60-20,
解得:y=10,
点P第二次旋转到直线AB上的时间为:(40+180)÷10=22s,
若此时相遇,则22y=60,
解得:y=![]() ,
,
答:点Q运动的速度为10cm/s或![]() cm/s.
cm/s.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】公园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 15元 | 13元 | 11元 |
某校七年级(1)(2)两个班共102人去游园,其中(1)班超过40人,不足50人,经估算,如果两个班都以班为单位购票,则一共应付1422元.问:
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可比两个班都以班为单位购票省多少元钱?
(2)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?