��Ŀ����
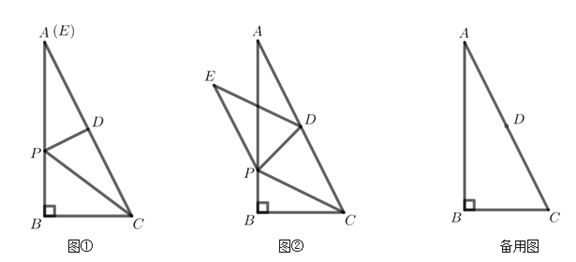
����Ŀ����Rt��ABC�У���B=90�㣬BC=4��AB=8����D�DZ�AC���е㣬����P�ڱ�AB��(��P�����A�غ�)������PD��PC������PDC��ֱ��PD���ۣ���C���ڵ�E���á�PDE��
��1����ͼ�٣�����Eǡ�����A�غϣ����߶�AP�ij���
��2����ͼ�ڣ���ED��AB�ڵ�F���ı���CDEPΪ���Σ���֤����PFE�ա�AFD��
��3������AE�����PDE���ABC�ص����ֵ����ΪS1����PAC�����ΪS2����S1=![]() S2ʱ����ֱ��д��tan��AED��ֵ��
S2ʱ����ֱ��д��tan��AED��ֵ��
���𰸡���1��AP=5����2��֤������������3��3��![]() ��
��
��������
��1�����ݷ��۵����ʵ�AP=PC����AP=x�����ݹ��ɶ����г����̣����x��ֵ���ɣ�
��2���������ε����ʵó�PE��CD��PE=CD���ڸ��ݴ�������D��AC���е�ɵó�AD=PE��PE��AC��Ȼ���Ƴ���PFE�ա�AFD��
��3������S1=![]() S2�Ƴ�AF=PF��EF=DF��Ȼ������������������ͼ���ٹ�D��DM��AP�ڵ�M����C��CN��PD�ڵ�N���ڹ�D��DM��AP�ڵ�M���ٷֱ���㼴�ɣ�
S2�Ƴ�AF=PF��EF=DF��Ȼ������������������ͼ���ٹ�D��DM��AP�ڵ�M����C��CN��PD�ڵ�N���ڹ�D��DM��AP�ڵ�M���ٷֱ���㼴�ɣ�
��1���ߡ�PDE�ɡ�PDC��������
��AP=PC��
��AP=x��
�ߡ�B=90�㣬
����Rt��PBC��PC2=PB2+BC2��
��x2=��8-x��2+42��
���x=5��
��AP=5��
��2�����ı���CDPEΪ���Σ�
��PE��CD��PE=CD��
��D��AC���е㣬
��AD=CD��
��AD=PE��
��PE��CD��
��PE��AC��
���APE=��PAD����DEP=��ADE��
�ڡ�PFE���AFD��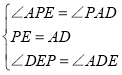 ��
��
���PFE�ա�AFD��
��3����D��AC�����꣬
��S��ADP=S��CDP=![]() S��PAC��
S��PAC��
���۵��ɵã�S��PDE=S��CDP��
��S��PDF=![]() S��PAC=
S��PAC=![]() S��ADP=
S��ADP=![]() S��PDE��
S��PDE��
��AF=PF��EF=DF��
����ͼ���ı���AEPD��ƽ���ı��Σ�
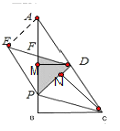
��D��DM��AP�ڵ�M����C��CN��PD�ڵ�N��
���AED=��EDP=��PDC��
�ߣ���B=90�㣬BC=4��AB=8��
��AC=![]() ��
��
��PC=PE=AD=![]() ��
��
��PB=![]() ��
��
��BM=![]() AB=4��DM=
AB=4��DM=![]() BC=2����λ�ߣ���
BC=2����λ�ߣ���
��PM=BM-PB=2��
��DP=![]() ��
��
��DN=![]() ��CN=
��CN=![]() ��
��
��tan��AED=tan��PDC=![]() =3��
=3��
����ͼ����D��DM��AP�ڵ�M
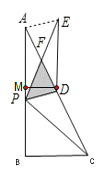 ��
��
��AP=DE=DC=![]() ��
��
��PM=![]() -4��
-4��
��tan��AED=tan��DPM=![]() ��
��
���ϣ�tan��AED��ֵΪ3��![]() ��
��

 ����ѧ����ϵ�д�
����ѧ����ϵ�д�