题目内容
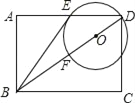
【题目】已知:如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD,BD分别交于点E、点F,且∠ABE=∠DBC.
(1)判断直线BE与⊙O的位置关系,并证明你的结论;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
【答案】(1)直线BE与⊙O相切,证明见解析;(2)⊙O的半径为![]() .
.
【解析】分析:(1)连接OE,根据矩形的性质,可证∠BEO=90°,即可得出直线BE与⊙O相切;
(2)连接EF,先根据已知条件得出BD的值,再在△BEO中,利用勾股定理推知BE的长,设出⊙O的半径为r,利用切线的性质,用勾股定理列出等式解之即可得出r的值.
详解:(1)直线BE与⊙O相切.理由如下:
连接OE,在矩形ABCD中,AD∥BC,∴∠ADB=∠DBC.
∵OD=OE,∴∠OED=∠ODE.
又∵∠ABE=∠DBC,∴∠ABE=∠OED,
∵矩形ABDC,∠A=90°,∴∠ABE+∠AEB=90°,
∴∠OED+∠AEB=90°,∴∠BEO=90°,∴直线BE与⊙O相切;
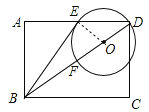
(2)连接EF,方法1:
∵四边形ABCD是矩形,CD=2,∴∠A=∠C=90°,AB=CD=2.
∵∠ABE=∠DBC,∴sin∠CBD=![]()
∴![]() ,
,
在Rt△AEB中,∵CD=2,∴![]() .
.
∵tan∠CBD=tan∠ABE,∴![]() ,
,
由勾股定理求得![]() .
.
在Rt△BEO中,∠BEO=90°,EO2+EB2=OB2.
设⊙O的半径为r,则![]() ,∴r=
,∴r=![]() ,
,
方法2:∵DF是⊙O的直径,∴∠DEF=90°.
∵四边形ABCD是矩形,∴∠A=∠C=90°,AB=CD=2.
∵∠ABE=∠DBC,∴sin∠CBD=![]() .
.
设![]() ,则
,则![]() .
.
span>∵CD=2,∴![]() .
.
∵tan∠CBD=tan∠ABE,∴![]() ,
,
∴E为AD中点.
∵DF为直径,∠FED=90°,∴EF∥AB,∴![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() .
.