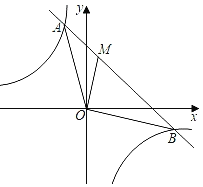
题目内容
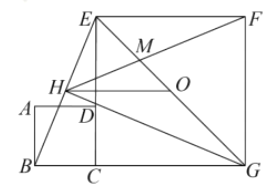
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,OA=3,OC=2,且BE∥AC,AE∥OB.
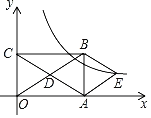
(1)求证:四边形AEBD是菱形;
(2)求经过点E的双曲线对应的函数解析式;
(3)设经过点E的双曲线与直线BE的另一交点为F,过点F作x轴的平行线,交经过点B的双曲线于点G,交y轴于点H,求△OFG的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先证明四边形AEBD是平行四边形,再证明DA=DB,即可得出结论;
(2)求出点E的坐标,即可求解;
(3)根据△OFG的面积S=S△OHG﹣S△OHF,即可求解.
解:(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形.
∵四边形OABC是矩形,
∴DA=![]() AC,DB=
AC,DB=![]() OB,AC=OB.
OB,AC=OB.
∴DA=DB.
∴平行四边形AEBD是菱形.
(2)如图1,连接DE,交AB于点M,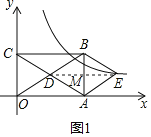
∵四边形AEBD是菱形,
∴AB与DE互相垂直且平分.
∵OA=3,OC=2,
∴EM=DM=![]() OA=
OA=![]() ,AM=
,AM=![]() AB=1.
AB=1.
∴点E的坐标为(![]() ,1).
,1).
设经过点E的反比例函数解析式为y=![]() ,
,
把点E(![]() ,1)代得k=
,1)代得k=![]() ,
,
∴双曲线的函数解析式为y=![]() .
.
(3)设经过点B的反比例函数解析式为y=![]() ,
,
把点B(3,2)代入得k1=6,
∴经过点B的反比例函数解析式为y=![]() .
.
∵直线FG∥x轴(如图2),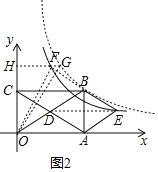
△OFG的面积S=S△OHG-S△OHF=![]() |k1|-
|k1|-![]() |k|=
|k|=![]() ×6-
×6-![]() ×
×![]() .
.

【题目】由于世界人口增长、水污染以及水资源浪费等原因,全世界面临着淡水资源不足的问题,我国是世界上严重缺水的国家之一.节约用水是水资源合理利用的关键所在,是最快捷、最有效、最可行的维护水资源可持续利用的途径之一,为了调查居民的用水情况,有关部门对某小区的20户居民的月用水量进行了调查,数据如下(单位![]() ):
):
6.7 8.7 7.3 11.4 7.0 6.9 11.7 9.7 10.0 9.7
7.3 8.4 10.6 8.7 7.2 8.7 10.5 9.3 8.4 8.7
整理数据:按如下分段整理样本数据并补充表格(表1):
用水量 |
|
|
|
|
人数 |
| 6 | b | 4 |
分析数据:补全下列表格中的统计量(表2):
平均数 | 中位数 | 众数 |
8.85 |
| 8.7 |
得出结论:
(1)表中的![]() ,
,![]() ,
,![]() ;
;
(2)若用表1中的数据制作一个扇形统计图,![]() 所占的扇形圆心角的度数为 度;
所占的扇形圆心角的度数为 度;
(3)如果该小区有住户400户,根据样本估计用水量在![]() 的居民有多少户?
的居民有多少户?