题目内容
【题目】如图1,在![]() 中,弦
中,弦![]() 弦
弦![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() .
.
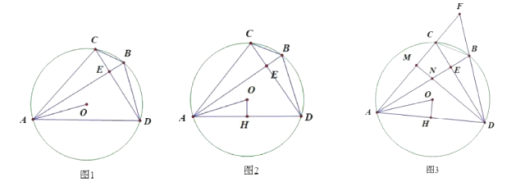
(1)求证:![]()
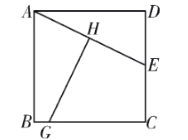
(2)如图2,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,求证:
,求证:![]()
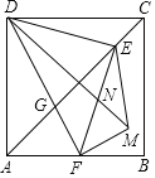
(3)如图3,在(2)的条件下,延长![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接OB,OD,利用圆周角定理结合三角形内角和定理可得结果;
(2)过O作OT⊥BC于T,连接OB,OC,在ED上找点G,使得CE=EG,连接BG,证明![]() ,得到OH=BT,设∠BDC=α,利用垂直平分线的性质得到BC=BG,结合三角形外角的性质得到BC=BG=GD,从而可得结果;
,得到OH=BT,设∠BDC=α,利用垂直平分线的性质得到BC=BG,结合三角形外角的性质得到BC=BG=GD,从而可得结果;
(3)在AF上作点Q,使得AQ=BQ,连接BQ,OQ,过B作BW⊥AF于点W,设BF=x,则AF=3x,推出△QBF为直角三角形,利用勾股定理得出AQ、BQ、BW、FW、AW的表达式,从而得到![]() ,
,![]() ,设BE=n,则DE=3n,EG=3n-12,在△BEG中,利用勾股定理求出n的值,得到BE、DE、EG、EC的值,利用三角函数算出NE的长,再证明△CBE∽△ADE,得到
,设BE=n,则DE=3n,EG=3n-12,在△BEG中,利用勾股定理求出n的值,得到BE、DE、EG、EC的值,利用三角函数算出NE的长,再证明△CBE∽△ADE,得到![]() ,算出AE,从而得到AN,最后在△AMN利用勾股定理求出MN的长.
,算出AE,从而得到AN,最后在△AMN利用勾股定理求出MN的长.
解:(1)连接OB,OD,
∵AD=AB,
∴弧AC=弧AD,
∴∠AOB=∠AOD,
∴∠OAB=∠OBA,∠OAD=∠ODA,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
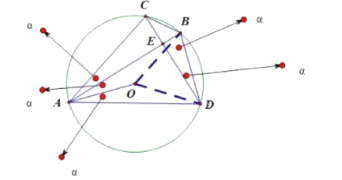
(2)过O作OT⊥BC于T,连接OB,OC,在ED上找点G,使得CE=EG,连接BG,
∵∠COB=2∠CAB,∠CAB=∠CDB,∠AOB=∠AOD,![]() ,
,
∴2∠OAH=2∠BAO=∠COB,
∵OC=OB,OT⊥BC,
∴∠OAH=∠BOT,
又∵∠OTB=∠OHA=90°,OB=OA,
∴![]() ,
,
∴OH=BT,
∵BC=2BT,
∴2OH=BC,
设∠BDC=α,
∴∠BCD=∠BAD=2α,
∵CE=GE,AB⊥CD,
∴BC=BG,则∠BGC=∠BCG=2α,
∵∠BDC=α,
∴∠GBD=α,
∴BC=BG=GD,
∴DE=EG+GD=CE+BC=CE+2OH,
即![]() ;
;
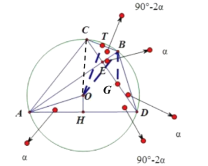
(3)在AF上作点Q,使得AQ=BQ,连接BQ,OQ,过B作BW⊥AF于点W,
∵AQ=BQ,OA=OB,
∴OQ垂直平分AB,
∴∠QAB=∠QBA,
∵AF=3BF,设BF=x,则AF=3x,
∵AB⊥CD,
∴∠ACD+∠CAB=90°,
∵∠ACD=∠ABD,
∴∠ABD+∠ABQ=90°,
∴△QBF为直角三角形,
设AQ=QB=a,则FQ=3x-a,在△QBF中,
![]() ,解得:
,解得:![]() ,
,
即AQ=BQ=![]() ,QF=
,QF=![]() ,
,
∴BW=BF×BQ÷QF=![]() ,
,
∴FW=![]() ,
,
∴AW=AF-FW=![]() ,
,
∴![]() ,
,![]() ,
,
由(2)知:BC=BG=DG=12,CE=EG,
∴BE=ED·tan∠BDC,
设BE=n,则DE=3n,EG=3n-12,
在△BEG中,![]() ,
,
解得:n=![]() 或0(舍),
或0(舍),
∴BE=![]() ,DE=
,DE=![]() ,EG=EC=
,EG=EC=![]() ,
,
在△DMC和△BDE中,
∠MCD=∠EBD,∠DMC=∠DEB,
∴∠MDC=∠EDB,
∴tan∠MDC=tan∠EDB=tan∠CAB=![]() ,
,
∴NE=DE×![]() =
=![]() ,
,
∵∠BCE=∠BAD,∠CBE=∠ADE,
∴△CBE∽△ADE,
∴![]() ,
,
∴AE=3CE=![]() ,
,
∴AN=AE-NE=![]() ,
,
∴设MN=m,则AM=3m,在△AMN中,
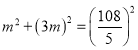 ,
,
解得:m=![]() 或
或![]() (舍)
(舍)
∴![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】声音在空气中传播的速度y(米/秒)是气温x (摄氏度)的一次函数,下表列出了一组不同气温时的音速.
气温x/摄氏度 | 0 | 5 | 10 | 15 | 20 |
音速y/(米/秒) | 331 | 334 | 337 | 340 | 343 |
(1)求y 与 x之间的函数关系式
(2)气温x=22(摄氏度)时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地相距多远?