题目内容
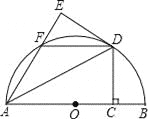
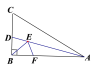
【题目】如图,在Rt△ABC中,AB=6, ∠BAC=30, ∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是___
【答案】3
【解析】
作FG⊥AD交AC于点G,交AD于点Q,连接BG交AD于点E,作BH⊥AC,易证∠BAD=∠CAD,即可证明△AQG≌△AQF,可得AF=AG,再证明△AEF≌△AEG,可得EG=EF,即可求得BE+EF=BG,当BG与BH重合时BG最短,由此即可求解.
作FG⊥AD交AC于点G,交AD于点Q,连接BG交AD于点E,作BH⊥AC与点H,
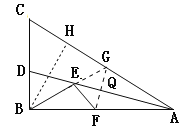
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△AQG和△AQF中,
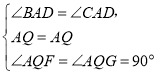 ,
,
∴△AQG≌△AQF(ASA),
∴AF=AG,
在△AEF和△AEG中,
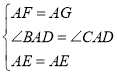 ,
,
∴△AEF≌△AEG(SAS),
∴EG=EF,
∴BE+EF=BE+EG=BG,
∴当BG与BH重合时,BG最短,
即BE+EF的最小值为BH的长,
∵AB=6,∠BAC=30°,
∴BH=![]() AB=3,
AB=3,
即BE+EF的最小值是3.
故答案为:3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?