Question

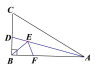
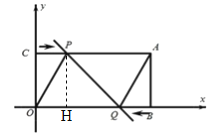
【题目】如图，在平面直角坐标系 xOy 中，点 A 是一次函数 y 3x 20 与 y x 12的交点，过点 A 分别作 x 、 y 轴的垂线段，垂足分别是 B 和C ，动点 P 和Q 以1个单位/秒的速度，分别从点C 、 B 出发，沿线段CA 、 BO 方向，向终点 A 、O 运动，设运动时间为t秒.

（1）证明：无论运动时间t 0 t 8取何值，四边形OPAQ 始终为平行四边形；

（2）当四边形OPAQ 为菱形时，请求出此时 PQ 的长度及直线 PQ 的函数解析式；

（3）当OP 满足 2 OP 5时，连接 PQ ，直线 PQ 与 y 轴交于点 M ，取线段 AC 的中点 N ，试确定 MNP 的面积 S 与运动的时间t 之间的函数关系式，并求出 S 的取值范围.

Answer 1

【答案】（1）证明见解析；（2），y=－2x+10；（3）S=t（2≤t≤3），2≤S≤3．

【解析】

（1）根据一组对边平行且相等的四边形是平行四边形判断即可；

（2）过P作PH⊥x轴于H，则CP=OH，PH=CO．解方程组求出A的坐标，由菱形的性质以及勾股定理求得t的值，进而得到OQ、OH，HQ的长．利用勾股定理即可求出PQ的长，利用待定系数法可得到直线PQ的解析式．

（3）分别计算出当OP=和OP=5时，对应的t的值，即可得出t的取值范围．

再利用相似三角形的判定与性质表示出MC，然后利用三角形面积公式即可得出结论．

（1）∵0 t 8，∴CP=QB=t．

∵CA=OB，∴PA=OQ．

∵PA∥OQ，∴四边形OPAQ为平行四边形．

（2）过P作PH⊥x轴于H，则CP=OH，PH=CO．

解方程组得：，∴A（8，4），∴CO=BA=4，OB=CA=8．

∵四边形OPAQ 为菱形，∴OP=PA=OQ=8-t．在Rt△CPO中，∵OC2+CP2=OP2，∴，解得：t=3，∴OQ=8-t=5，OH=CP=3，∴HQ=OQ-OH=5-3=2．

∵PH=CO=4，∴PQ===．

∵CP=3，OQ=5，∴P（3，4），Q（5，0）．设直线PQ的解析式为y=kx+b，∴，解得：，∴．设直线PQ的解析式为y=－2x+10．

（3）当OP=时，CP==2，∴t=2；

当OP=5时，CP==3，∴t=3；∴2≤t≤3．

∵CP∥OQ，∴△MCP∽△MOQ，∴，∴，解得：MC=．

∵CA=8，∴CN=4，∴PN=4－t，∴△MNP的面积S=PNCM==t，∴S=t（2≤t≤3），∴2≤S≤3．