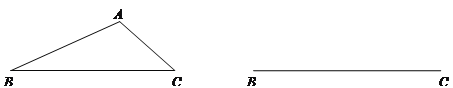Question

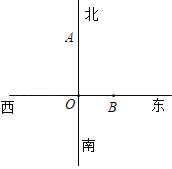
【题目】阅读理解：数和形是数学的两个主要研究对象，我们经常运用数形结合，树形转化的方法解决一些数学问题，小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用图1得到结论：P1P2=，他还利用图2证明了线段P1P2的中点P（x，y），P的坐标公式：x=，y=．

启发应用：

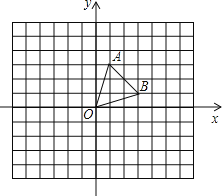
如图3：在平面直角坐标系中，已知A（8，0），B（0，6），C（1，7），⊙M经过原点O及点A，B，

（1）求⊙M的半径及圆心M的坐标；

（2）判断点C与⊙M的位置关系，并说明理由；

（3）若∠BOA的平分线交AB于点N，交⊙M于点E，分别求出OE的表达式y1，过点M的反比例函数的表达式y2，并根据图象，当y2＞y1＞0时，请直接写出x的取值范围．

Answer 1

【答案】（1）⊙M的半径为5，M（4，3）；（2）点C在⊙M上，理由见解析；（3）y2= ，，y2＞y1＞0时，0＜x＜2

【解析】试题分析：（1）先确定出AB=10，进而求出圆M的半径，最后用线段的中点坐标公式即可得出结论；
（2）求出CM=5和圆M的半径比较大小，即可得出结论；
（3）先确定出直线和双曲线解析式，即可求出两图象的交点坐标，即可得出结论．

试题解析：

（1）∵∠AOB=90°，

∴AB是⊙M的直径，

∵A（8，0），B（0，6），

∴AB==10，

∴⊙M的半径为5，

由线段中点坐标公式x=，y=，得x=4，y=3，

∴M（4，3），

（2）点C在⊙M上，

理由：∵C（1，7），M（4，3），

∴CM==5，

∴点C在⊙M上；

（3）由题意知，y1=x，

设反比例函数的解析式为y2=（k≠0），

∵M（4，3）在反比例函数图象上，

∴k=3×4=12，

∴反比例函数的解析式为y2= ，

当y1=y2时，x=，

∴x=±2，

∴由图象知，当y2＞y1＞0时，0＜x＜2 ．