题目内容
如图,在直角梯形ABCD中,AD∥BC,AD⊥DC,点A关于对角线BD的对称点F刚好落在腰DC上,连接AF交BD于点E,AF的延长线与BC的延长线交于点G,M,N分别是BG,DF的中点.

(1)求证:四边形EMCN是矩形;
(2)若AD=2,S梯形ABCD= ,求矩形EMCN的长和宽.
,求矩形EMCN的长和宽.

(1)求证:四边形EMCN是矩形;
(2)若AD=2,S梯形ABCD=
 ,求矩形EMCN的长和宽.
,求矩形EMCN的长和宽.解:(1)证明:∵点A、F关于BD对称,∴AD=DF,DE⊥AF。
又∵AD⊥DC,∴△ADF、△DEF是等腰直角三角形。∴∠DAF=∠EDF=45°。
∵AD∥BC,∴∠G=∠GAF=45°。∴△BGE是等腰直角三角形。
∵M,N分别是BG,DF的中点,∴EM⊥BC,EN⊥CD。
又∵AD∥BC,AD⊥DC,∴BC⊥CD。∴四边形EMCN是矩形。
(2)由(1)可知,∠EDF=45°,BC⊥CD,∴△BCD是等腰直角三角形。∴BC=CD,
∴S梯形ABCD= (AD+BC)•CD=
(AD+BC)•CD= (2+CD)•CD=
(2+CD)•CD= ,即CD2+2CD﹣15=0。
,即CD2+2CD﹣15=0。
解得CD=3,CD=﹣5(舍去)。
∵△ADF、△DEF是等腰直角三角形,∴DF=AD=2。
∵N是DF的中点,∴EN=DN= DF=
DF= ×2=1。
×2=1。
∴CN=CD﹣DN=3﹣1=2。
∴矩形EMCN的长和宽分别为2,1。
又∵AD⊥DC,∴△ADF、△DEF是等腰直角三角形。∴∠DAF=∠EDF=45°。
∵AD∥BC,∴∠G=∠GAF=45°。∴△BGE是等腰直角三角形。
∵M,N分别是BG,DF的中点,∴EM⊥BC,EN⊥CD。
又∵AD∥BC,AD⊥DC,∴BC⊥CD。∴四边形EMCN是矩形。
(2)由(1)可知,∠EDF=45°,BC⊥CD,∴△BCD是等腰直角三角形。∴BC=CD,
∴S梯形ABCD=
 (AD+BC)•CD=
(AD+BC)•CD= (2+CD)•CD=
(2+CD)•CD= ,即CD2+2CD﹣15=0。
,即CD2+2CD﹣15=0。解得CD=3,CD=﹣5(舍去)。
∵△ADF、△DEF是等腰直角三角形,∴DF=AD=2。
∵N是DF的中点,∴EN=DN=
 DF=
DF= ×2=1。
×2=1。∴CN=CD﹣DN=3﹣1=2。
∴矩形EMCN的长和宽分别为2,1。
试题分析:(1)根据轴对称的性质可得AD=DF,DE⊥AF,判断出△ADF、△DEF是等腰直角三角形,根据等腰直角三角形的性质求出∠DAF=∠EDF=45°,根据两直线平行,内错角相等求出∠BCE=45°,然后判断出△BGE是等腰直角三角形,根据等腰直角三角形的性质可得EM⊥BC,EN⊥CD,再根据矩形的判定证明即可。
(2)判断出△BCD是等腰直角三角形,然后根据梯形的面积求出CD的长,再根据等腰直角三角形的性质求出DN,即可得解。

练习册系列答案
相关题目

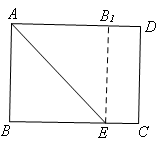


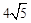 ,BC=4,向矩形ABCD外作△CDE,使△CDE为等腰三角形,且点E在边BC所在的直线上,请你画出图形,直接写出OE的长,并画出体现解法的辅助线.
,BC=4,向矩形ABCD外作△CDE,使△CDE为等腰三角形,且点E在边BC所在的直线上,请你画出图形,直接写出OE的长,并画出体现解法的辅助线.
 ,则AP的长为_____.
,则AP的长为_____.