题目内容
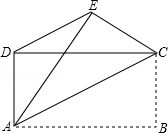
如图,四边形ABCD是等腰梯形,下底AB在x轴上,点D在y轴上,直线AC与y轴交于点E(0,1),点C的坐标为(2,3).
(1)求A、D两点的坐标;
(2)求经过A、D、C三点的抛物线的函数关系式;
(3)在y轴上是否在点P,使△ACP是等腰三角形?若存在,请求出满足条件的所有点P的坐标;若不存在,请说明理由.

(1)求A、D两点的坐标;
(2)求经过A、D、C三点的抛物线的函数关系式;
(3)在y轴上是否在点P,使△ACP是等腰三角形?若存在,请求出满足条件的所有点P的坐标;若不存在,请说明理由.

(1)点A的坐标为(﹣1,0)。点D的坐标为(0,3)。
(2)y=x2﹣2x+3。
(3)存在。满足条件的点P有5个,分别为:P1(0,2),P2(0, ),P3(0,
),P3(0, ),P4(0,
),P4(0, ),P5(0,
),P5(0, )。
)。
(2)y=x2﹣2x+3。
(3)存在。满足条件的点P有5个,分别为:P1(0,2),P2(0,
 ),P3(0,
),P3(0, ),P4(0,
),P4(0, ),P5(0,
),P5(0, )。
)。试题分析:(1)利用待定系数法求出直线EC的解析式,确定点A的坐标;然后利用等腰梯形的性质,确定点D的坐标。
(2)利用待定系数法求出抛物线的解析式。
(3)满足条件的点P存在,且有多个,需要分类讨论:
①作线段AC的垂直平分线,与y轴的交点,即为所求;
②以点A为圆心,线段AC长为半径画弧,与y轴的两个交点,即为所求;
③以点C为圆心,线段CA长为半径画弧,与y轴的两个交点,即为所求。
解:(1)设直线EC的解析式为y=kx+b,
根据题意得:
 ,解得
,解得 。
。∴y=x+1,
当y=0时,x=﹣1,∴点A的坐标为(﹣1,0)。
∵四边形ABCD是等腰梯形,C(2,3),∴点D的坐标为(0,3)。
(2)设过A(﹣1,0)、D(0,3)、C(2,3)三点的抛物线的解析式为y=ax2+bx+c,则有:
 ,解得
,解得 。
。∴抛物线的关系式为:y=x2﹣2x+3。
(3)存在。
①作线段AC的垂直平分线,交y轴于点P1,交AC于点F,

∵OA=OE,
∴△OAE为等腰直角三角形,∠AEO=45°。
∴∠FEP1=∠AEO=45°。
∴△FEP1为等腰直角三角形。
∵A(﹣1,0),C(2,3),点F为AC中点,
∴F(
 )。
)。∴等腰直角三角形△FEP1斜边上的高为
 。
。∴EP1=1。∴P1(0,2)。
②以点A为圆心,线段AC长为半径画弧,交y轴于点P2,P3.
可求得圆的半径长AP2=AC=3
 ,
,连接AP2,则在Rt△AOP2中,
 ,
,∴P2(0
 ).
).∵点P3与点P2关于x轴对称,∴P3(0,
 ).
).③以点C为圆心,线段CA长为半径画弧,交y轴于点P4,P5,
则圆的半径长CP4=CA=3
 ,
,在Rt△CDP4中,CP4=3
 ,CD=2,
,CD=2,∴
 。
。∴OP4=OD+DP4=
 。∴P4(0,
。∴P4(0, ).
).同理,可求得:P5(0,
 )。
)。综上所述,满足条件的点P有5个,分别为:P1(0,2),P2(0,
 ),P3(0,
),P3(0, ),P4(0,
),P4(0, ),P5(0,
),P5(0, )。
)。
练习册系列答案
相关题目
 AD,CF=
AD,CF=



 ,求矩形EMCN的长和宽.
,求矩形EMCN的长和宽.
 ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是
ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是
 的值为
的值为