题目内容
菱形ABCD中,∠A=60°,AB=6,点P是菱形内一点,PB=PD= ,则AP的长为_____.
,则AP的长为_____.
 ,则AP的长为_____.
,则AP的长为_____. 或
或
试题分析:根据题意得,先根据特殊角的锐角三角函数值求得PM的长,再分P与A在BD的同侧与异侧两种情况进行讨论,即可求得结果.
解:当P与A在BD的异侧时,连接AP交BD于M,

∵AD=AB,DP=BP,
∴AP⊥BD(到线段两端距离相等的点在垂直平分线上),
在直角△ABM中,∠BAM=30°,
∴AM=AB•cos30°=3
 ,BM=AB•sin30°=3,
,BM=AB•sin30°=3,∴PM=
 ,
,∴AP=AM+PM=
 ;
;当P与A在BD的同侧时,连接AP并延长AP交BD于点M

AP=AM-PM=
 ;
;当P与M重合时,PD=PB=3,与PB=PD=
 矛盾,舍去.
矛盾,舍去.所以AP的长为
 或
或 .
.点评:本题注意到应分两种情况讨论,并且注意两种情况都存在关系AP⊥BD,这是解决本题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目

 ,求矩形EMCN的长和宽.
,求矩形EMCN的长和宽. 中,已知
中,已知 平分
平分 交
交 边于点
边于点 ,则
,则 等于
等于

 ABCD的周长为l6cm,对角线AC与BD相交于点O,
ABCD的周长为l6cm,对角线AC与BD相交于点O, 交AD于E,连接CE,则△DCE的周长为( )
交AD于E,连接CE,则△DCE的周长为( )
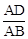 的值为
的值为