题目内容
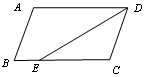
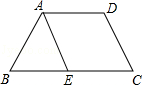
如图,在等腰梯形ABCD中,AD∥BC,AE∥DC,AE=6cm,且∠B=60°.则下列说法中错误的是( )

| A.△ABE是等边三角形 | B.四边形AECD是菱形 |
| C.E不一定为BC的中点 | D.CD的长必为6cm |
B
试题分析:根据等腰梯形的性质可以得到△ABE是等边三角形,而四边形AECD是平行四边形,然后根据菱形的定义,即可作出判断.
解:∵等腰梯形ABCD,AD∥BC,
又∵AE∥CD,
∴四边形AECD是平行四边形.
∴AE=CD,
∵AB=CD,
∴AB=AE=CD=6,故D正确.
又∵∠B=60°,
∴△ABE是等边三角形.故A正确;
E不一定为BC的中点正确,
则AE=EC不一定成立,故C正确,B错误.
故选B.
点评:本题考查了等腰梯形的性质以及平行四边形、等边三角形的判定定理,理解△ABE是等边三角形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 AD,CF=
AD,CF=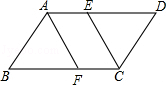
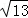 .
.


 ,求矩形EMCN的长和宽.
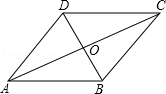
,求矩形EMCN的长和宽. ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是
ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是
 中,已知
中,已知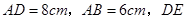 平分
平分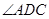 交
交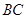 边于点
边于点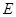 ,则
,则 等于
等于