题目内容
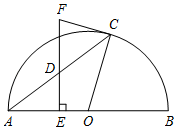
【题目】如图1,△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F是DE与AC的交点,且DF=FE.
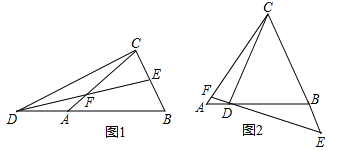
(1)图1中是否存在与∠BDE相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
(2)求证:BE=EC;
(3)若将“点D在BA的延长线上,点E在BC上”和“点F是DE与AC的交点,且DF=FE”分别改为“点D在AB上,点E在CB的延长线上”和“点F是ED的延长线与AC的交点,且DF=kFE”,其他条件不变(如图2).当AB=1,∠ABC=a时,求BE的长(用含k、a的式子表示).
【答案】(1)∠DCA=∠BDE.(2)证明见解析;(3)![]() .
.
【解析】
试题(1)运用等腰三角形的性质及三角形的外角性质就可解决问题.
(2)过点E作EG∥AC,交AB于点G,如图1,要证BE=CE,只需证BG=AG,由DF=FE可证到DA=AG,只需证到DA=BG即DG=AB,也即DG=AC即可.只需证明△DCA≌△△EDG即可解决问题.
(3)过点A作AH⊥BC,垂足为H,如图2,可求出BC=2cosα.过点E作EG∥AC,交AB的延长线于点G,易证△DCA≌△△EDG,则有DA=EG,CA=DG=1.易证△ADF∽△GDE,则有![]() .由DF=kFE可得DE=EF-DF=(1-k)EF.从而可以求得AD=
.由DF=kFE可得DE=EF-DF=(1-k)EF.从而可以求得AD=![]() ,即GE=
,即GE=![]() ,易证△ABC∽△GBE,则有
,易证△ABC∽△GBE,则有![]() ,从而可以求出BE.
,从而可以求出BE.
试题解析:(1)∠DCA=∠BDE.
证明:∵AB=AC,DC=DE,
∴∠ABC=∠ACB,∠DEC=∠DCE.
∴∠BDE=∠DEC-∠DBC=∠DCE-∠ACB=∠DCA.
(2)过点E作EG∥AC,交AB于点G,如图1,
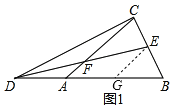
则有∠DAC=∠DGE.
在△DCA和△EDG中,
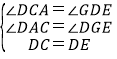
∴△DCA≌△EDG(AAS).
∴DA=EG,CA=DG.
∴DG=AB.
∴DA=BG.
∵AF∥EG,DF=EF,
∴DA=AG.
∴AG=BG.
∵EG∥AC,
∴BE=EC.
(3)过点E作EG∥AC,交AB的延长线于点G,如图2,

∵AB=AC,DC=DE,
∴∠ABC=∠ACB,∠DEC=∠DCE.
∴∠BDE=∠DBC-∠DEC=∠ACB-∠DCE=∠DCA.
∵AC∥EG,
∴∠DAC=∠DGE.
在△DCA和△EDG中,
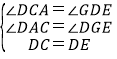
∴△DCA≌△EDG(AAS).
∴DA=EG,CA="DG"
∴DG=AB=1.
∵AF∥EG,
∴△ADF∽△GDE.
∴![]()
∵DF=kFE,
∴DE=EF-DF=(1-k)EF.
∴![]() .
.
∴AD=![]()
∴GE=AD=![]()
过点A作AH⊥BC,垂足为H,如图2,
∵AB="AC,AH⊥BC,"
∴BH="CH."
∴BC="2BH."
∵AB="1,∠ABC=α,"
∴BH=ABcos∠ABH="cosα."
∴BC="2cosα."
∵AC∥EG,
∴△ABC∽△GB.
∴![]() .
.
∴![]() .
.
∴BE=![]() .
.
∴BE的长为![]() .
.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案