Question

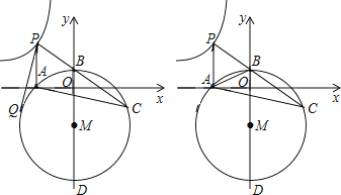
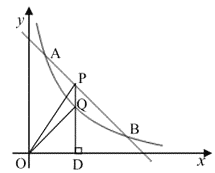
【题目】如图，一次函数y=kx+b与反比例函数（x>0)的图象交于点A(a，3)和B(3，1）．

（1）求一次函数的解析式．

（2）观察图象，写出反比例函数值小于一次函数值时x的取值范围．

（3）点P是线段AB上一点，过点P作PD⊥x轴于点D，交反比例函数图象于点Q，连接OP、OQ，若△POQ的面积为，求P点的坐标。

Answer 1

【答案】（1）y=-x+4；（2）1<x<3；（3）P（2，2）

【解析】

（1）将B(3，1）代入反比例函数式中，求出K'，即得反比例函数解析式，将A(a，3)代入y= 中，得出a=1，即得A（1，3）,最后将A（1，3）与B(3，1）分别代入y=kx+b中，求出k、b的值即可.

（2）反比例函数值小于一次函数值，即是反比例函数图像在一次函数图象下方时的x的范围，利用图象直接读出即可.

（3）设P（m，-m+4），则Q（m，），可得PQ=-m+4-， 根据S△POQ= ×m×PQ=建立方程，解出m即可.

（1）解：把 代入 中，得 ，∴

把 代入 中，得 ，∴

把 、 代入 中，得：

解得

∴

（2）解：由图象得：

（3）解：设 且 ，则

∴

∴

解得

∴