Ő‚ńŅńŕ»›
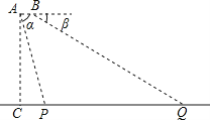
°ĺŐ‚ńŅ°Ņ‘ŕĺō–őABCD÷–£¨AB£Ĺ5 cm£¨BC£Ĺ6 cm£¨Ķ„Pī”Ķ„AŅ™ ľ—ōABŌÚ÷’Ķ„B“‘1 cm/sĶńňŔ∂»“∆∂Į£¨”ŽīňÕ¨ Ī£¨Ķ„Qī”Ķ„BŅ™ ľ—ōĪŖBCŌÚ÷’Ķ„C“‘2 cm/sĶńňŔ∂»“∆∂Į£¨»ÁĻŻP°ĘQ∑÷Īūī”A°ĘBÕ¨ Ī≥Ų∑Ę£¨ĶĪĶ„Q‘ň∂ĮĶĹĶ„C Ī£¨ŃĹĶ„Õ£÷Ļ‘ň∂Į£¨…Ť‘ň∂Į Īľšő™t√Ž£ģ
(1)ŐÓŅ’£ļBQ£Ĺ________£¨PB£Ĺ________(”√ļ¨tĶńīķ ż ĹĪŪ ĺ)£Ľ
(2)ĶĪtő™ļő÷Ķ Ī£¨PQĶń≥§∂»Ķ»”ŕ![]() cm?
cm?
(3) «∑Ůīś‘ŕtĶń÷Ķ£¨ ĻĶ√őŚĪŖ–őAPQCDĶń√śĽżĶ»”ŕ26 cm2£Ņ»Űīś‘ŕ£¨«Ž«ů≥Ųīň ĪtĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ

°ĺīūįł°Ņ£®1£©2t cm£Ľ(5£≠t)cm£Ľ£®2£©ĶĪt£Ĺ3√Ž Ī£¨PQĶń≥§∂»Ķ»”ŕ![]() cm£Ľ£®3£©īś‘ŕ£¨ĶĪt£Ĺ1√Ž Ī£¨őŚĪŖ–őAPQCDĶń√śĽżĶ»”ŕ26 cm2£¨ņŪ”…ľŻĹ‚őŲ£ģ
cm£Ľ£®3£©īś‘ŕ£¨ĶĪt£Ĺ1√Ž Ī£¨őŚĪŖ–őAPQCDĶń√śĽżĶ»”ŕ26 cm2£¨ņŪ”…ľŻĹ‚őŲ£ģ
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›P°ĘQŃĹĶ„Ķń‘ň∂ĮňŔ∂»Ņ…Ķ√BQ°ĘPBĶń≥§∂»£Ľ
£®2£©łýĺ›ĻīĻ…∂®ņŪŅ…Ķ√PB2+BQ2£ĹQP2£¨īķ»ŽŌŗ”¶ żĺ›Ĺ‚∑Ĺ≥ŐľīŅ…£Ľ
£®3£©łýĺ›Ő‚“‚Ņ…Ķ√°ųPBQĶń√śĽżő™≥§∑Ĺ–őABCDĶń√śĽżľű»•őŚĪŖ–őAPQCDĶń√śĽż£¨‘Ŕłýĺ›»żĹ«–őĶń√śĽżĻę Ĺīķ»ŽŌŗ”¶ŌŖ∂őĶń≥§ľīŅ…Ķ√ĶĹ∑Ĺ≥Ő£¨‘ŔĹ‚∑Ĺ≥ŐľīŅ…£ģ
Ĺ‚£ļ(1) °ŖPī”Ķ„AŅ™ ľ—ōĪŖABŌÚ÷’Ķ„B“‘1cm/sĶńňŔ∂»“∆∂Į£¨
°ŗAP£Ĺtcm£ģ
°ŖAB£Ĺ5cm£¨
°ŗPB£Ĺ(5©Āt)cm£ģ
°ŖĶ„Qī”Ķ„BŅ™ ľ—ōĪŖBCŌÚ÷’Ķ„C“‘2cm/sĶńňŔ∂»“∆∂Į£¨
°ŗBQ£Ĺ2tcm£¨
Ļ īūįłő™£ļ2t cm £¨(5£≠t)cm £Ľ
°°(2)”…Ő‚“‚Ķ√£ļ(5£≠t)2£ę(2t)2£Ĺ(![]() )2£¨
)2£¨
Ĺ‚Ķ√t1£Ĺ-1(≤ĽļŌŐ‚“‚£¨…Š»•)£¨t2£Ĺ3£ģ
ĶĪt£Ĺ3√Ž Ī£¨PQĶń≥§∂»Ķ»”ŕ![]() cm£ģ°°
cm£ģ°°
(3)īś‘ŕ£ģ ņŪ”…»ÁŌ¬£ļ
≥§∑Ĺ–őABCDĶń√śĽż «£ļ5°Ń6£Ĺ30(cm2)£¨
ĻĶ√őŚĪŖ–őAPQCDĶń√śĽżĶ»”ŕ26 cm2£¨
‘Ú°ųPBQĶń√śĽżő™30£≠26£Ĺ4(cm2)£¨
°ŗ(5£≠t) °Ń2t°Ń![]() £Ĺ4£¨
£Ĺ4£¨
Ĺ‚Ķ√t1£Ĺ4(≤ĽļŌŐ‚“‚£¨…Š»•)£¨t2£Ĺ1£ģ
ľīĶĪt£Ĺ1√Ž Ī£¨ ĻĶ√őŚĪŖ–őAPQCDĶń√śĽżĶ»”ŕ26 cm2£ģ

 ľ‚◊”…ķ–¬ŅőŐ√Ņő Ī◊ų“ĶŌĶŃ–īūįł
ľ‚◊”…ķ–¬ŅőŐ√Ņő Ī◊ų“ĶŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņń≥–£”–3000√Ż—ß…ķ£ģő™ŃňĹ‚»ę–£—ß…ķĶń…Ō—ß∑Ĺ Ĺ£¨ł√–£ ż—ß–ň»§–°◊ť“‘ő ĺŪĶų≤ťĶń–ő Ĺ£¨ňśĽķĶų≤ťŃňł√–£≤Ņ∑÷—ß…ķĶń÷ų“™…Ō—ß∑Ĺ Ĺ(≤ő”Žő ĺŪĶų≤ťĶń—ß…ķ÷Ľń‹ī”“‘Ō¬ŃýłŲ÷÷ņŗ÷–—°‘Ů“Ľņŗ)£¨≤ĘĹęĶų≤ťĹŠĻŻĽś÷∆≥…»ÁŌ¬≤ĽÕÍ’ŻĶńÕ≥ľ∆Õľ£ģ
÷÷ņŗ | A | B | C | D | E | F |
…Ō—ß∑Ĺ Ĺ | ĶÁ∂Į≥Ķ | ňĹľ“≥Ķ | ĻęĻ≤ĹĽÕ® | ◊‘––≥Ķ | ≤Ĺ–– | ∆šňŻ |
ń≥–£≤Ņ∑÷—ß…ķ÷ų“™…Ō—ß∑Ĺ Ĺ…»–őÕ≥ľ∆Õľń≥–£≤Ņ∑÷—ß…ķ÷ų“™…Ō—ß∑Ĺ ĹŐű–őÕ≥ľ∆Õľ

łý囓‘…Ō–ŇŌĘ£¨ĽōīūŌ¬Ń–ő Ő‚£ļ
(1)≤ő”ŽĪĺīőő ĺŪĶų≤ťĶń—ß…ķĻ≤”–____»ň£¨∆š÷–—°‘ŮBņŗĶń»ň ż”–____»ň£ģ
(2)‘ŕ…»–őÕ≥ľ∆Õľ÷–£¨«ůEņŗ∂‘”¶Ķń…»–ő‘≤–ńĹ«¶ŃĶń∂» ż£¨≤Ę≤Ļ»ęŐű–őÕ≥ľ∆Õľ£ģ
(3)»ŰĹęA°ĘC°ĘD°ĘE’‚ňńņŗ…Ō—ß∑Ĺ Ĺ ”ő™°į¬Ő…ę≥Ų––°Ī£¨«ŽĻņľ∆ł√–£√ŅŐž°į¬Ő…ę≥Ų––°ĪĶń—ß…ķ»ň ż£ģ