题目内容
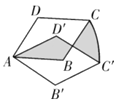
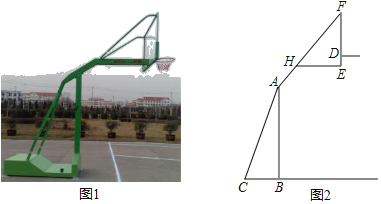
【题目】已知:如图,AD⊥BC,垂足为D,AD=BD,点E在AD上,∠CED=45°,
(1)请写出图中相等的线段: .(不包括已知条件中的相等线段)
(2)猜想BE与AC的位置关系,并说明理由.
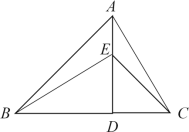
【答案】(1)DE=DC,BE=AC;(2)互相垂直,理由见解析
【解析】
(1)根据题目中的条件和图形,可以证明△BDE≌△ADC,从而可以得到对应边相等,本题得以解决;
(2)根据△BDE≌△ADC和直角三角形的性质,可以得到BE与AC的位置关系.
(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠CED=45°,
∴∠ECD=45°,
∴∠ECD=∠CED,
∴DE=DC,
在△BDE和△ADC中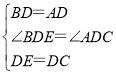
∴△BDE≌△ADC(SAS)
∴BE=AC,
由上可得,图中相等的线段:DE=DC,BE=AC,
故答案为:DE=DC,BE=AC;
(2)BE与AC的位置关系是互相垂直,
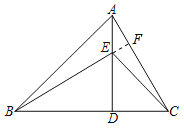
理由:由(1)知,△BDE≌△ADC,
则∠DBE=∠DAC,
∵∠EDB=90°,
∴∠DBE+∠DEB=90°,
∵∠DEB=∠AEF,
∴∠DBE+∠AEF=90°,
∴∠DAC+∠AEF=90°,
∴∠AFE=90°,
∴BF⊥AC,
即BE与AC的位置关系是互相垂直.

练习册系列答案
相关题目