题目内容
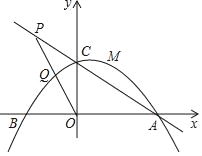
【题目】如图,抛物线y=﹣![]() (其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(1)求△AOC的周长,(用含m的代数式表示)
(2)若点P为直线AC上的一点,且点P在第二象限,满足OP2=PCPA,求tan∠APO的值及用含m的代数式表示点P的坐标;
(3)在(2)的情况下,线段OP与抛物线相交于点Q,若点Q恰好为OP的中点,此时对于在抛物线上且介于点C与抛物线顶点之间(含点C与顶点)的任意一点M(x0,y0)总能使不等式n≤![]() 及不等式2n﹣
及不等式2n﹣![]() 恒成立,求n的取值范围.
恒成立,求n的取值范围.
【答案】(1) 3m+3![]() m;(2)tan∠APO=
m;(2)tan∠APO=![]() ,P(﹣
,P(﹣![]() );(3)
);(3) ![]() ≤n≤2.
≤n≤2.
【解析】
(1)分别令x=0和y=0,计算抛物线与两坐标轴的交点C和A的坐标,再根据勾股定理计算AC的长,根据三角形的周长可得结论;
(2)根据特殊三角函数值可得∠CAO=30°,证明△OPA∽△CPO,则∠POC=∠OAC=30°,可得tan∠APO=![]() ,过P作PE⊥x轴于E,表示OE和PE的长,根据点P在第二象限,可得P的坐标;
,过P作PE⊥x轴于E,表示OE和PE的长,根据点P在第二象限,可得P的坐标;
(3)根据中点坐标公式可得Q的坐标,代入抛物线的解析式可得m的值,计算对称轴,得x0的取值范围,根据两个不等式确定其解集即可.
(1)当x=0时,y=﹣![]() ×
×![]() ×(﹣3m)=
×(﹣3m)=![]() m,∴C(0,
m,∴C(0,![]() m),∴OC=
m),∴OC=![]() m,当y=0时,﹣
m,当y=0时,﹣![]() =0,解得:x1=﹣
=0,解得:x1=﹣![]() ,x2=3m.
,x2=3m.
∵A在B的右侧,其中m>0,∴A(3m,0),由勾股定理得:AC=![]() =
=![]() =2
=2![]() m,∴△AOC的周长=OA+OC+AC=3m+
m,∴△AOC的周长=OA+OC+AC=3m+![]() m+2
m+2![]() m=3m+3
m=3m+3![]() m;
m;
(2)Rt△AOC中,tan∠OAC=![]() =
=![]() =
=![]() ,∴∠CAO=30°.
,∴∠CAO=30°.
∵OP2=PCPA,∴![]() .
.
∵∠OPC=∠OPC,∴△OPA∽△CPO,∴∠POC=∠OAC=30°.
∵∠ACO=∠POC+∠APO,∴∠APO=60°﹣30°=30°,∴tan∠APO=![]() .
.
过P作PE⊥x轴于E.
∵∠APO=∠OAC=30°,∴PO=OA=3m,∠POE=60°,Rt△PEO中,∠EPO=30°,∴OE=![]() OP=
OP=![]() ,PE=
,PE=![]() .
.
∵点P在第二象限,∴P(﹣![]() );
);
(3)由(2)知:P(﹣![]() ).
).
∵点Q恰好为OP的中点,∴Q(﹣![]() ).
).
∵Q在抛物线上,则![]() =﹣
=﹣![]() ,解得:m=
,解得:m=![]() ,∴抛物线的解析式为:y=﹣
,∴抛物线的解析式为:y=﹣![]() (x+
(x+![]() )(x﹣3
)(x﹣3![]() )=﹣
)=﹣![]() ,对称轴是:x=﹣
,对称轴是:x=﹣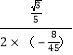 =
=![]() ,作抛物线的对称轴交抛物线于点F.
,作抛物线的对称轴交抛物线于点F.
∵M在点C与顶点F之间(含点C与顶点F),∴0≤x0≤![]() ,n≤
,n≤![]() ,设w1=
,设w1=![]() .
.
∵1>0,∴w1随x0的增大而增大,∴当x0=![]() 时,w1有最大值,即
时,w1有最大值,即![]() 有最小值为2,∴n≤2,对于不等式2n﹣
有最小值为2,∴n≤2,对于不等式2n﹣![]() ,n≥﹣2
,n≥﹣2![]() ,n≥﹣2(x0﹣
,n≥﹣2(x0﹣![]() )2+
)2+![]() ,设w2=﹣2(x0﹣
,设w2=﹣2(x0﹣![]() )2+
)2+![]() .
.
∵﹣2<0,∴w2有最大值.
∵0<![]() <
<![]() ,∴当x0=
,∴当x0=![]() 时,w2有最大值为
时,w2有最大值为![]() ,∴n≥
,∴n≥![]() .
.
综上所述:n的取值范围是![]() ≤n≤2.
≤n≤2.

【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小亮做摸球试验,他将盒子内的球搅匀后从中随机摸出一个球,记下颜色后放回,不断重复上述过程,对试验结果进行统计后,小玲得到下表中的数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 1500 |
摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
摸到白球的频率 | 0.70 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
则下列结论中正确的是( )
A. n越大,摸到白球的概率越接近0.7
B. 当n=2000时,摸到白球的次数m=1200
C. 当n很大时,摸到白球的频率将会稳定在0.6附近
D. 这个盒子中约有28个白球