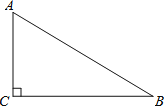
题目内容
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——应用函数解决问题”的学习过程.在画函数图象时,我们可以通过描点或平移的方法画出一个函数的大致图象,结合上面经历的学习过程,现在来解决下面问题:
在函数![]() 中,当
中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;
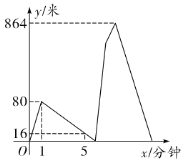
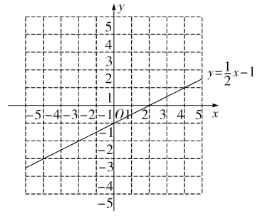
(3)已知函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
【答案】(1)![]() ;(2)画出函数图象见解析; ①函数
;(2)画出函数图象见解析; ①函数![]() 在
在![]() 时,
时,![]() 随
随![]() 的增大而减小;②函数
的增大而减小;②函数![]()
![]() 在
在![]() 时,
时,![]() 的值不变;(3)
的值不变;(3)![]() 的解集为
的解集为![]() .
.
【解析】
(1)把点直接代入函数解析式,列出方程组求解即可得出;
(2)根据描点,连线的方法画出函数图象,结合图象,可以看出①在![]() 时,
时,![]() 随
随![]() 的增大而减小;②在
的增大而减小;②在![]() 时,
时,![]() 的值不变;
的值不变;
(3)从图象可以直接得出![]() 图象在上方时,所对应的x的取值范围即可得出结果.
图象在上方时,所对应的x的取值范围即可得出结果.
(1)∵在函数![]() 中,当
中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
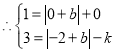 ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
∴这个函数的表达式为![]() ,
,
故答案为:![]() ;
;
(2)画出函数图象如图:
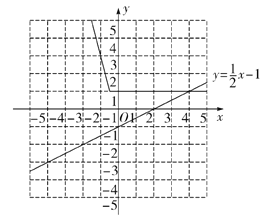
函数的性质(写出其中一条即可):①函数![]() 在
在![]() 时,
时,![]() 随
随![]() 的增大而减小;②函数
的增大而减小;②函数![]() 在
在![]() 时,
时,![]() 的值不变,
的值不变,
故答案为:在![]() 时,
时,![]() 随
随![]() 的增大而减小;在
的增大而减小;在![]() 时,
时,![]() 的值不变;
的值不变;
(3)由函数图象可得:![]() 的解集为
的解集为![]() ,
,
故答案为:![]() .
.

 寒假学与练系列答案
寒假学与练系列答案【题目】某文具店每天售出甲、乙两种笔,统计后发现:甲、乙两种笔同一天售出量之间满足一次函数的关系,设甲、乙两种笔同一天的售出量分别为x(支)、y(支),部分数据如表所示(下表中每一列数据表示甲、乙两种笔同一天的售出量).
甲种笔售出x(支) | … | 4 | 6 | 8 | … |
乙种笔售出y(支) | … | 6 | 12 | 18 | … |
(1)求y关于x的函数关系式;(不需要写出函数的定义域)
(2)某一天文具店售出甲、乙两种笔的营业额分别为30元和120元,如果乙种笔每支售价比甲种笔每支售价多2元,那么甲、乙两种笔这天各售出多少支?