Question

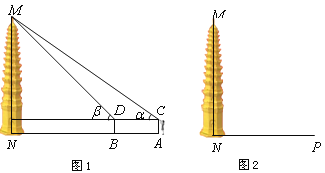
【题目】如图，某建筑物上挂着“巴山渝水，魅力重庆”的宣传条幅，王同学利用测倾器在斜坡的底部处测得条幅底部的仰角为60°，沿斜坡AB走到B处测得条幅顶部C的仰角为50°．已知斜坡的坡度米，米（点在同平面内，，测倾器的高度忽略不计），则条幅的长度约为（参考数据：）

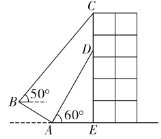
A.12.5米B.12.8米C.13.1米D.13.4米

Answer 1

【答案】B

【解析】

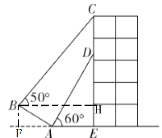
过点B作BF⊥AE于点F，BH⊥DE于点H，在Rt△AFB中，由坡度和勾股定理可以求出BF、AF的长度，在Rt△BHC中，利用三角函数求出CH，再求出DH，最后用CH-DH求出CD即可．

如图所示：

过点B作BF⊥AE于点F，BH⊥DE于点H，

∵的坡度m，

∴，，

∴，BF为边长，

∴解得BF=5，则AF=12m，

∵AE=12m，

∴EF=AF+AE=24（m），

∵∠BHE=∠HEF=∠BFE=90°，

∴四边形BFEH是矩形，

∴EH=BF=5m，BH=EF=24m，

在Rt△BHC中，∠CBH=50°，

∴CH=BH24×1.19=28.56（m），

在Rt△ADE中，∠DAE=60°，

∴DE=AE=12×20.76（m），

∴CD=CH-DH=28.56-(20.76-5)=12.8（m），

∴条幅CD的长度约为12.8m，

故选：B．