题目内容
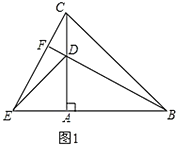
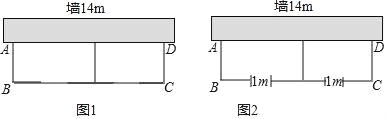
【题目】如图，有长为22米的篱笆，一面利用墙（墙的最大可用长度为14米），围成中间隔有一道篱笆的长方形花圃，有以下两种围法．
（1）如图1，设花圃的宽AB为x米，面积为y米2，求y与x之间的含函数表达式，并确定x的取值范围；
（2）如图2，为了方便出入，在建造篱笆花圃时，在BC上用其他材料造了宽为1米的两个小门，设花圃的宽AB为a米，面积为S米2，求S与a之间的函数表达式及S的最大值？
【答案】（1）y=﹣3x2+22x（
≤x＜
）；（2）S=﹣3a2+24a（
≤a＜8），当a=4时，S最大值为48．
【解析】
（1）设花圃的宽AB为x米，由矩形面积y=长×宽，列出函数解析式；
（2）由在BC上用其他材料造了宽为1米的两个小门，故长变为22﹣3a+2，再列出函数解析式．
（1）设花圃的宽AB为x米，面积为y米2，y=ABBC=x（22﹣3x）
=﹣3x2+22x．
根据题意可得：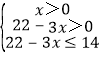
，解得：≤x＜，即x的取值范围：≤x＜；
（2）设花圃的宽AB为a米，面积为S米2，由题意可得：S=a（22﹣3a+2）
=﹣3a2+24a=﹣3（a﹣4）2+48．
根据题意可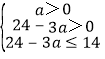得：
，解得：≤a＜8，即x的取值范围：≤a＜8，当a=4时，S最大值为48．
【题目】某公司生产一种原料，运往A地和B地销售．如表记录的是该产品运往A地和B地供应量y1（kg）、y2（kg）与销售价格x（元）之间的关系：
销售价格x（元） | 100 | 150 | 200 | 300 |
运往A地y1（kg） | 300 | 250 | 200 | 100 |
运往B地y2（kg） | 450 | 350 | 250 | n |
（1）请认真分析上表中所给数据，用你所学过的函数来表示其变化规律，并验证你的猜想，分别求出y1与x、y2与x的函数关系式；
（2）用你求出的函数关系式完成上表，直接写出n＝ ；
（3）直接写出销售价格在 元时，该产品运往A地的供应量等于运往B地的供应量．
