题目内容
如图,在平面直角坐标系xoy中,以点M(1,-1)为圆心,以 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经过点A、B、C,顶点为E.
的图象经过点A、B、C,顶点为E.
(1)求此二次函数的表达式;
(2)设∠DBC=a,∠CBE=b,求sin(a-b)的值;
(3)坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1) ;(2)
;(2) ;(3)P1(0,0),P2(0,
;(3)P1(0,0),P2(0, ),P3(9,0).
),P3(9,0).
解析试题分析:(1)由M(1,-1)为圆心,半径为 可求出A(-1,0)、B(3,0)、C(0,-3)、D(0,1),把A、B、C三点代入二次函数解析式求出a、b、c的值即可;
可求出A(-1,0)、B(3,0)、C(0,-3)、D(0,1),把A、B、C三点代入二次函数解析式求出a、b、c的值即可;
(2)在Rt△BCE中与Rt△BOD中可求出∠CBE=∠OBD=b,故sin(a-b)=sin(∠DBC-∠OBD)=sin∠OBC= ;
;
(3)存在,Rt△COA∽Rt△BCE,此时点P1(0,0)过A作AP2⊥AC交y正半轴于P2,由Rt△CAP2 ∽Rt△BCE,得P2(0, ),过C作CP3⊥AC交x正半轴于P3,由Rt△P3CA∽Rt△BCE,得P3(9,0)故在坐标轴上存在三个点P1(0,0),P2(0,
),过C作CP3⊥AC交x正半轴于P3,由Rt△P3CA∽Rt△BCE,得P3(9,0)故在坐标轴上存在三个点P1(0,0),P2(0, ),P3(9,0),.
),P3(9,0),.
试题解析:(1)∵M(1,-1)为圆心,半径为
∴OA=1,OB=3,OC=3,OD=1,
∴A(-1,0)、B(3,0)、C(0,-3)、D(0,1)
把A(-1,0)、B(3,0)、C(0,-3)代入二次函数y=ax2+bx+c
解得:a=1,b=-2,c=-3
∴ 二次函数表达式为
(2)过点E作EF⊥y轴于点F
∵
∴可得
∵点E为二次函数 的顶点
的顶点
∴点E的坐标为
∴
∵
∴∠OCB=∠ECF=45º
∴∠BCE=90º
∵在Rt△BCE中与Rt△BOD中,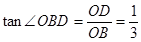 ,
,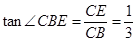
∴∠CBE=∠OBD=b,
∴ sin(a-b)=sin(∠DBC-∠OBD)=sin∠OBC=
(3)显然 Rt△COA∽Rt△BCE,此时点P1(0,0)
过A作AP2⊥AC交y正半轴于P2,由Rt△CAP2 ∽Rt△BCE,得P2(0, )
)
过C作CP3⊥AC交x正半轴于P3,由Rt△P3CA∽Rt△BCE,得P3(9,0)
故在坐标轴上存在三个点P1(0,0),P2(0, ),P3(9,0),使得以P、A、C为顶点的三角形与BCE相似
),P3(9,0),使得以P、A、C为顶点的三角形与BCE相似
考点:1.二次函数解析式;2.相似三角形的判定与性质.

 是△
是△ 中
中 的角平分线,
的角平分线, 是
是 上的一点,且
上的一点,且 ,
, ,
, .
.
 ∽△
∽△ ;
; ∽△
∽△ ;
; 的长.
的长.
 的值;
的值; 的值.
的值.

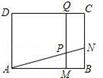
 ),解答下列问题:
),解答下列问题:
 为何值时,PQ∥BC?
为何值时,PQ∥BC? ),求y与t之间的函数关系式;
),求y与t之间的函数关系式; ,求
,求 的值.
的值. 
 ,那么
,那么
 ,那么
,那么 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).

 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.