题目内容
如图,正△ABC中,∠ADE=60°,
(1)求证:△ABD∽△DCE;
(2)若BD=2,CD=4,求AE的长.
(1)证明见解析;(2)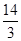 .
.
解析试题分析:(1)在正ABC中,由∠ADE=60°,可知∠ADB+∠EDC=120°,∠BAD+∠ADB=120°,所以∠BAD=∠EDC,又∠B=∠C,可证得△ABD∽△DCE;
(2)由(1)根据相似三角形的对应边成比例,可求得CE的长,从而求出AE的长.
试题解析:(1)在正ABC中,∠B=∠C=60°
∵∠BAD+∠ADB=120°,∠EDC+∠ADB=180°-∠ADE=120°
∴∠BAD=∠EDC
∵∠B=∠C
∴△ABD∽△DCE.
(2)∵△ABD∽△DCE,
∴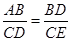
∴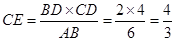
∴AE=AC-CE=6- =
=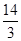
考点:1.等边三角形的性质;2.相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
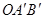 与△OAB是以O为位似中心的位似图形,且位似比为1︰3.
与△OAB是以O为位似中心的位似图形,且位似比为1︰3.
 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经过点A、B、C,顶点为E.
的图象经过点A、B、C,顶点为E.



 ;
;
 ;
;
 是等边三角形,点
是等边三角形,点 、
、 分别在边
分别在边 、
、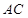 上,
上, .
.
 ∽△
∽△ ;(2)如果
;(2)如果 ,
, ,求
,求 的长.
的长.