题目内容
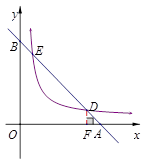
如图,已知直线l分别与x轴、y轴交于A、B两点,与双曲线 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4):
① 分别求出直线l与双曲线的解析式;(3分)
② 若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?(4分)
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.(2分)
(1)①反比例函数的解析式为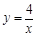 ,直线AB的解析式为y=-x+5;
,直线AB的解析式为y=-x+5;
②当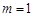 时,直线l与反比例函数有且只有一个交点;
时,直线l与反比例函数有且只有一个交点;
(2)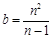
解析试题分析:(1)、①把点D或点E的坐标代入双曲线 (a≠0,x>0)中,易求反比例函数的解析式为
(a≠0,x>0)中,易求反比例函数的解析式为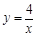 ,设直线AB的解析式为y=ax+b,再把点D或点E的坐标代入,可得一个二元一次方程组,求得直线AB的解析式为y = -x+5;
,设直线AB的解析式为y=ax+b,再把点D或点E的坐标代入,可得一个二元一次方程组,求得直线AB的解析式为y = -x+5;
② 依题意可设向下平移m(m>0)个单位后解析式为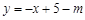 ,直线l与双曲线有且只有一个交点即
,直线l与双曲线有且只有一个交点即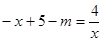 (整理得
(整理得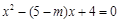 )的△=0即△=
)的△=0即△=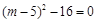 ,
,
解得: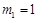 ,
,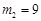 (舍去),即当
(舍去),即当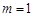 时,直线l与反比例函数有且只有一个交点;
时,直线l与反比例函数有且只有一个交点;
(2)、过点D作DF⊥OA于F(如下图),则△ADF∽△ABO得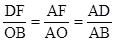 ,即
,即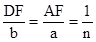 解得:DF=
解得:DF=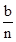 ,AF=
,AF=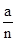 ;所以OF=OA-AF=a-
;所以OF=OA-AF=a-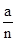 =
=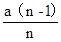 ,所以点D的坐标为(
,所以点D的坐标为(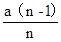 ,
,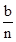 ),又因为点D在双曲线
),又因为点D在双曲线 (a≠0,x>0)上,所以
(a≠0,x>0)上,所以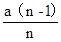 ×
×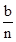 =a,所以
=a,所以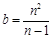 .
.
试题解析:(1) ①易求反比例函数的解析式为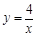 ,
,
直线AB的解析式为y = -x+5;(5分)
② 依题意可设向下平移m(m>0)个单位后解析式为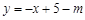 ,
,
由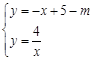 ,得
,得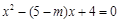 ,
,
∵ 平移后直线l与反比例函数有且只有一个交点,∴△=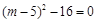 ,
,
∴ 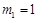 ,
,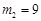 (舍去).
(舍去).
即当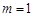 时,直线l与反比例函数有且只有一个交点;(5分)
时,直线l与反比例函数有且只有一个交点;(5分)
(2) 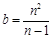 .(2分)
.(2分)
考点:1、用待定系数法求一次函数与反比例函数的解析式;2、一元二次方程;3、相似三角形.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经过点A、B、C,顶点为E.
的图象经过点A、B、C,顶点为E.

 ;
;
 是等边三角形,点
是等边三角形,点 、
、 分别在边
分别在边 、
、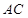 上,
上, .
.
 ∽△
∽△ ;(2)如果
;(2)如果 ,
, ,求
,求 的长.
的长.
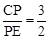 ,BP′=
,BP′= 时,求线段AB的长.
时,求线段AB的长.

 的值;
的值;
