题目内容
已知△ABC是等腰直角三角形,∠A=90°,点D是腰AC上的一个动点,过C作CE垂直于BD的延长线,垂足为E.
(1)若BD是AC边上的中线,如图1,求 的值;
的值;
(2)若BD是∠ABC的角平分线,如图2,求 的值.
的值.
(1)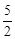 ;(2)2.
;(2)2.
解析试题分析:设AB=AC=1,CD=x,应用勾股定理和相似三角形的判定和性质,把 用x来表示,
用x来表示,
(1)若BD是AC的中线,则CD=AD,据此求出 的值;
的值;
(2)若BD是∠ABC的角平分线,则由Rt△ABD∽Rt△EBC得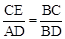 ,据此求出
,据此求出 的值.
的值.
试题解析:设AB=AC=1,CD=x,则0<x≤1,BC=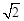 ,AD=1-x.
,AD=1-x.
在Rt△ABD中,BD2=AB2+AD2=1+(1-x)2=x2-2x+2.
由已知可得Rt△ABD∽Rt△ECD,
∴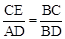 ,即
,即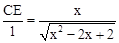 ,∴
,∴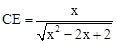 .
.
∴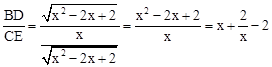 ,0<x≤1.
,0<x≤1.
(1)若BD是AC的中线,则CD=AD=x= ,得
,得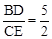 .
.
(2)若BD是∠ABC的角平分线,则Rt△ABD∽Rt△EBC,
∴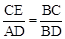 ,得
,得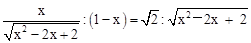 ,即
,即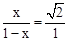 ,解得,
,解得,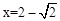 .
.
∴ .
.
考点:1.动点问题;2.等腰直角三角形的性质;3.勾股定理;4.相似三角形的判定和性质;5.三角形中线和角平分线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 =
= ,并写出点A2的坐标。
,并写出点A2的坐标。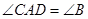 ,DC=3且
,DC=3且 ﹦1﹕2.
﹦1﹕2.
 的值.
的值. 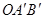 与△OAB是以O为位似中心的位似图形,且位似比为1︰3.
与△OAB是以O为位似中心的位似图形,且位似比为1︰3.
 ,求代数式
,求代数式 的值.
的值.
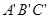 是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2).
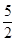 ,3),则A′的坐标为 ;②△ABC与△
,3),则A′的坐标为 ;②△ABC与△ 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经过点A、B、C,顶点为E.
的图象经过点A、B、C,顶点为E.

 ;
;