Question

【题目】已知，函数y＝ax2﹣6ax+9a+1与线段AB有交点，且已知点A（0，1）与点B（2，3）的坐标，则a的取值范围_____．

Answer 1

【答案】0≤a≤2．

【解析】

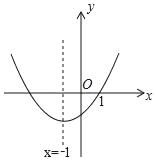
根据题意，函数与线段AB有交点，则可得出a≥0，结合图象得出a的临界值即可作答．

如图：

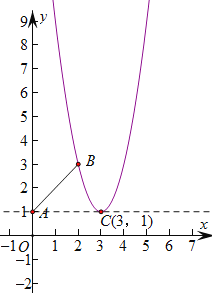
∵函数y＝ax2﹣6ax+9a+1＝a（x﹣3）2+1

∴顶点C（3，1）

∵函数y＝ax2﹣6ax+9a+1与线段AB有交点

∴当a＜0时函数与线段AB无交点

∴a≥0

①当a＝0时，函数y＝1，此时与线段AB的交点为点A，符合题意；

②当a＞0时：

若函数恰好经过点B，将点B（2，3）代入函数y＝ax2﹣6ax+9a+1＝a（x﹣3）2+1中解得：a＝2，此时a取最大值，

∵A（0，1），C（3，1）

∴直线AC∥x轴

∴当a＞0时，要使函数y＝ax2﹣6ax+9a+1与线段AB有交点，则a的范围是0＜a≤2；

综上所述：a的取值范围为0≤a≤2；

故答案为：0≤a≤2．