��Ŀ����
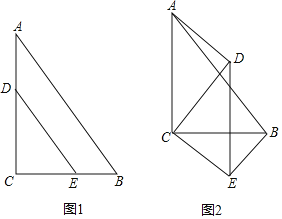
����Ŀ����ͼ1����Rt��ABC�У���C��90�㣬AC��8��AB��10��D��E����ֱ���AC��CB�ϵĵ㣬��CD��6��DE��AB������CDE�Ƶ�C˳ʱ����תһ�ܣ�����ת��Ϊ����
��1�����ⷢ��
�ٵ�����0��ʱ��![]() ���� ����
���� ����
�ڵ�����90��ʱ��![]() ���� ����
���� ����
��2����չ̽��
������뵱��CDE����ת�Ĺ����У�![]() �Ƿ����仯������ͼ2֤����IJ��룮
�Ƿ����仯������ͼ2֤����IJ��룮
��3��������
�ڽ���CDE�Ƶ�C˳ʱ����תһ�ܵĹ����У���AD��2![]() ʱ��BE���� ������ʱ������ ����
ʱ��BE���� ������ʱ������ ����
���𰸡���1����![]() ;��
;��![]() ;��2�����룺
;��2�����룺![]() ��ֵ����,���ɼ�����;��3��
��ֵ����,���ɼ�����;��3��![]() ��60���300�㣮
��60���300�㣮
��������
��1�������ù��ɶ������BC��������ƽ���߷��߶γɱ����������EC���ɽ�����⣮
����ȷ����ͼ�Σ����AD��BE���ɽ�����⣮
��2�����룺![]() ��ֵ���䣮�������������ε����ʼ��ɽ�����⣮
��ֵ���䣮�������������ε����ʼ��ɽ�����⣮
��3�����������Σ���AD��AC�����Ҳ࣬��AD��AC����࣬�ֱ���⼴�ɣ�
�⣺��1������ͼ1�У�������0ʱ��
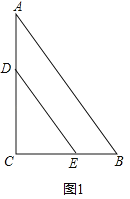
��Rt��ACB�У��ߡ�C��90����AC��8��AB��10��
��BC��![]() ��6��
��6��
��DE��AB��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��CE��![]() ��
��
��DE��AB��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
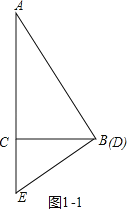
����ͼ1��1�У�������90��ʱ����֪AD��AB��10��BE��![]() ��
��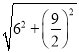 ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ![]() ��
��![]() ��
��
��2�����룺![]() ��ֵ���䣮
��ֵ���䣮
���ɣ���ͼ2�У�
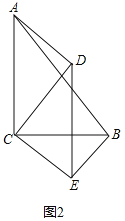
����ת�����У���DCE�ס�ACB��
���ACB����DCE��![]() ��
��![]() ��
��
��![]() ��
��![]() ����ACD����BCE��
����ACD����BCE��
���ACD�ס�BCE��
��![]() ��
��![]() ��
��![]() ��
��
��3����ͼ3��1�У���DH��AC��H����CH��x��
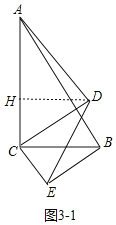
��DH2��AD2��AH2��CD2��CH2��
��52����8��x��2��62��x2��
���x��6��
��cos��HCD��![]() ��
��![]() ��
��
���ACD��60����
��![]() ��
��![]() ��AD��2
��AD��2![]() ��
��
��BE��![]() ����ʱ����60����
����ʱ����60����
��ͼ3��2�У�ͬ���ɵã���DCH��60����BE��![]() ����ʱ����300����
����ʱ����300����
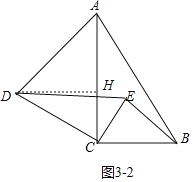
�ʴ�Ϊ��![]() ��60����300����
��60����300����

����Ŀ��Ϊ�˴���������У���ֹ2019��3����������17�Һ�����Է�鷿�������ѿ��ţ�ij�鷿Ϊ�˽�����Ķ����������������˲��ֶ�����һ���ڽ���ͼ��Ĵ��������Ƴ���ͼ��������ͳ��ͼ����
���߽���ͼ��Ĵ���ͳ�Ʊ�
����ͼ��Ĵ��� | 1�� | 2�� | 3�� | 4�� | 5�μ����� |
���� | 7 | 13 | a | 10 | 3 |
�������ͳ��ͼ���е���Ϣ������������⣺
��1��a���� ����b���� ����
��2���������ݵ�����Ϊ�� ������λ��Ϊ�� ����
��3�����������ͳ��ͼ�еġ�4�Ρ�����Ӧ��Բ�ĽǵĶ�����
��4����ͳ�Ƹ��鷿һ�ܹ���2000λ��ͬ�Ķ��ߣ��������ϵ���������������һ���ڽ���ͼ�顰4�μ����ϡ��Ķ���������