Question

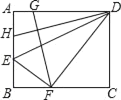
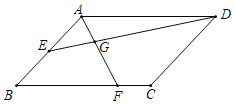
【题目】如图，平行四边形ABCD的边长AD＝3，AB＝2，∠BAD＝120°，E为AB的中点，F在边BC上，且BF＝2FC．AF与DE交于点G，则AG的长为_____．

Answer 1

【答案】

【解析】

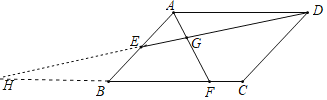
延长DE交直线BC于H，如图，利用平行四边形的性质和边长之间的关系证明△ABF为等边三角形得到AF＝AB＝2，再证明△ADE≌△BEH得到BH＝AD＝3，然后证明△ADG∽△FHG得到＝＝，最后利用比例性质计算出AG．

延长DE交直线BC于H，如图，

∵四边形ABCD为平行四边形，

∴BC＝AD＝3，AD∥BC，

∴∠B＝180°﹣∠BAD＝180°﹣120°＝60°，

∵AD＝3，AB＝2，BF＝2FC，

∴BF＝2＝AB，

∴△ABF为等边三角形，

∴AF＝AB＝2，

∵E为AB的中点，

∴AE＝BE，

而∠H＝∠ADE，∠AED＝∠BEH，

∴△ADE≌△BEH，

∴BH＝AD＝3，

∵AD∥FH，

∴△ADG∽△FHG，

∴＝＝，

∴＝，

∴AG＝×2＝．

故答案为．