��Ŀ����
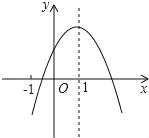
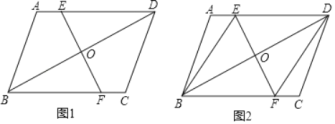
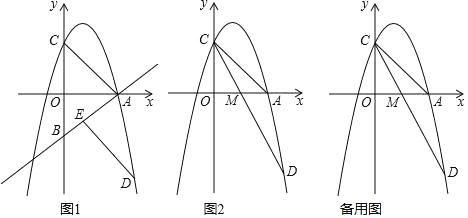
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��x��3��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B����B����x��ĶԳƵ���C�����κ���y����x2+bx+c��ͼ����A�͵�C��
��1������κ����ı���ʽ��
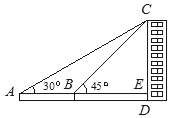
��2����ͼ1��ƽ���߶�AC����A�Ķ�Ӧ��D���ڶ��κ����ڵ�������ͼ���ϣ���C�Ķ�Ӧ��E����ֱ��AB�ϣ����ʱ��D�����ꣻ
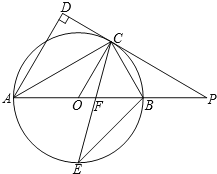
��3����ͼ2���ڣ�2���������£�����CD����CD���ڵ�M����PΪֱ��AC�Ϸ���������һ���㣬����P��PF��AC������Ϊ��F������PC���Ƿ���ڵ�P��ʹ���Ե�P��C��FΪ���������������COM���ƣ������ڣ����P�ĺ����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2+2x+3����2��D��4����5������3��![]() ��
��![]()
��������
��1����һ�κ����Ľ���ʽ���A��B�������꣬�ٸ���A��C�����������b��c����ȷ�����κ�������ʽ��
��2����ƽ�Ƶ�������E��m��m��3������D��m+3��m��6�������������ߵĽ���ʽ��������D�����ꣻ
��3��������������ۣ��١�COM�ס�PFC���ڡ�COM�ס�CFP������õ�P�ĺ����꣮
�⣺��һ�κ���y��x��3��ͼ����x�ᡢy��ֱ��ڵ�A��B���㣬
��A��3��0����B��0����3����
����B����x��ĶԳƵ���C��
��C��0��3����
�����κ���y����x2+bx+c��ͼ����A����C��
��![]() ��
��
��b��2��c��3��
�����κ����Ľ���ʽΪ��y����x2+2x+3��
��2����A��3��0����C��0��3����ƽ���߶�AC����A�Ķ�ӦΪ��D����C�Ķ�Ӧ��ΪE��
��E��m��m��3������D��m+3��m��6����
��D���ڶ��κ����ڵ�������ͼ���ϣ�
������m+3��2+2��m+3��+3��m��6��
m1��1��m2����6����ȥ����
��D��4����5����
��3����C��0��3����D��4����5����
��![]() ��
��
���![]() ��
��
��ֱ��CD�Ľ���ʽΪy����2x+3��
��y��0����x��![]() ��
��
��M��![]() ��0����
��0����
��һ�κ���y��x��3��ͼ����x�ύ��A��3��0����C ��0��3����
��AO��3��OC��3��
���OAC��45����
����P��PF��AC����P��PN��OA��AC�ڵ�E����PC��
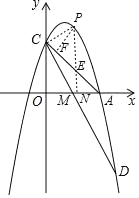
���PEF����AEN���ǵ���ֱ�������Σ�
��P��m����m2+2m+3����E��m����m+3����
��PE��PN��EN����m2+2m+3������m+3������m2+3m��
��EN����m+3��AE��![]() ��FE��
��FE��![]() ��
��
��CF��AC��AE��EF��![]() ��
��
������COM�ס�PFC�� ��
��
��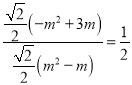 ��
��
���m1��0����ȥ��![]() ��
��
������COM�ס�CFPʱ��![]() ��
��
��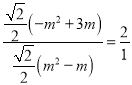 ��
��
���m1��0����ȥ����![]() ��
��
�ۺϿɵ�P��ĺ�����Ϊ![]() ��
��![]() ��
��