��Ŀ����
����Ŀ��ij���й���һ��ţ�����ۣ��������ۣ�ʵ�ʼ۸�ÿǧ�˱�ԭ����2Ԫ������ԭ��������ţ��32ǧ�˵�Ǯ�����ڿ���33ǧ�ˣ�
��1������ʵ�ʹ�������ţ��ÿǧ�˶���Ԫ��
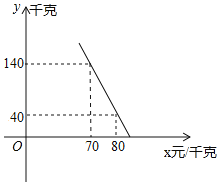
��2��������ţ���������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�������ͼ��ʾ��һ�κ�����ϵ����y��x֮��ĺ�����ϵʽ��
��3������ţ������۵��۶�Ϊ����ʱ���ܻ�����������������Ƕ��٣��������������멁������
���𰸡���1������ʵ�ʹ�������ţ��ÿǧ��64Ԫ����2����y����10x+840��������ţ������۵��۶�Ϊ74Ԫʱ���ܻ������������������1000Ԫ��
��������
��1��������ʵ�ʹ�������ţ��ÿǧ��xԪ������ԭ��������ţ��32ǧ�˵�Ǯ�����ڿ���33ǧ���г�����x��һԪһ�η��̣��ⷽ�̼��ɣ�
��2������y��x֮��ĺ�����ϵʽΪy=kx+b������70��1140������80��40�����룬���ô���ϵ�����������y��x֮��ĺ�����ϵʽ��
��������ţ������۵���ΪxԪʱ����������ΪwԪ����������=��������-�������õ�w����x�ĺ�����ϵʽΪw=-10��x-74��2+1000���ٸ��ݶ��κ��������ʼ�����⣮
��1��������ʵ�ʹ�������ţ��ÿǧ��aԪ����ԭ����������ţ��ÿǧ�ˣ�a+2��Ԫ�������⣬��
32��a+2����33a��
���a��64��
������ʵ�ʹ�������ţ��ÿǧ��64Ԫ��
��2������y��x֮��ĺ�����ϵʽΪy��kx+b��
����25��165������35��55�����룬
��![]() �����
�����![]() ��
��
��y��x֮��ĺ�����ϵʽΪy����10x+840��
��������ţ������۵���ΪxԪʱ����������ΪwԪ��
��w����x��64��y����x��64������10x+840������10x2+1480x��53760����10��x��74��2+1000��
���Ե�x��74ʱ��w�����ֵ1000��
�𣺽�����ţ������۵��۶�Ϊ74Ԫʱ���ܻ������������������1000Ԫ��

 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�