题目内容
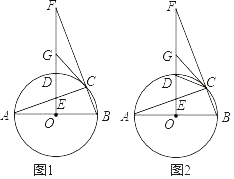
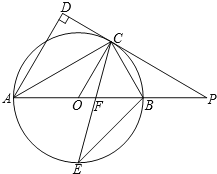
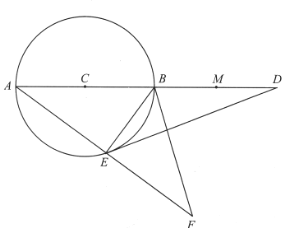
【题目】如图,AB是⊙C的直径,M、D两点在AB的延长线上,E是⊙C上的点,且DE2=DB· DA.延长AE至F,使AE=EF,设BF=10,cos∠BED=![]() .
.
(1)求证:△DEB∽△DAE;
(2)求DA,DE的长;
(3)若点F在B、E、M三点确定的圆上,求MD的长.
【答案】(1)证明见解析; (2)DA=![]() ,DE=
,DE=![]() ;(3)MD=
;(3)MD=![]() .
.
【解析】
(1)根据两边对应成比例且夹角相等的两个三角形相似进行判定即可;
(2)由直径所对的圆周角是直角可得BE⊥AF,再根据中垂线的性质可得AB=BF=10,由△DEB ∽△DAE,cos ∠BED=![]() ,可得cos ∠EAD =
,可得cos ∠EAD = ![]() ,在Rt△ABE中,解直角三角形可求得AE的长,BE的长,再由△DEB ∽△DAE,根据相似三角形的对应边成比例可得
,在Rt△ABE中,解直角三角形可求得AE的长,BE的长,再由△DEB ∽△DAE,根据相似三角形的对应边成比例可得 ![]() , 结合DB=DA-AB即可求得AD、DE的长;
, 结合DB=DA-AB即可求得AD、DE的长;
(3)连接FM,根据∠BEF=90°,根据90度角所对的弦是直径可确定出BF是B、E、F三点确定的圆的直径,再根据点F在B、E、M三点确定的圆上,可得四点F、E、B、M在同一个圆上,继而确定出点M在以BF为直径的圆上,在Rt△AMF中,由cos ∠FAM=![]() 可求得AM的长,再根据MD=DA-AM即可求得答案.
可求得AM的长,再根据MD=DA-AM即可求得答案.
(1)DE2=DB·DA,
∴![]() ,
,
又∵∠D=∠D,
∴△DEB∽△DAE;
(2)∵AB是⊙C的直径,E是⊙C上的点,
∴∠AEB=90°,即BE⊥AF,
又∵AE=EF,BF=10,
∴AB=BF=10,
∵△DEB ∽△DAE,cos ∠BED=![]() ,
,
∴∠EAD=∠BED,cos ∠EAD =cos ∠BED=![]() ,
,
在Rt△ABE中,由于AB=10,cos ∠EAD=![]() ,得AE=ABcos∠EAD=8,
,得AE=ABcos∠EAD=8,
∴![]() ,
,
∵△DEB ∽△DAE,
∴![]() ,
,
∵DB=DA-AB=DA-10,
∴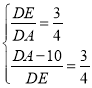 ,解得
,解得 ,
,
经检验, 是
是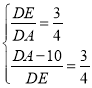 的解,
的解,
∴DA=![]() ,DE=
,DE=![]() ;
;
(3)连接FM,
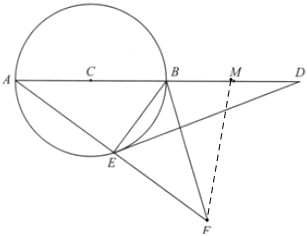
∵BE⊥AF,即∠BEF=90°,
∴BF是B、E、F三点确定的圆的直径,
∵点F在B、E、M三点确定的圆上,即四点F、E、B、M在同一个圆上,
∴点M在以BF为直径的圆上,
∴FM⊥AB,
在Rt△AMF中,由cos ∠FAM=![]() 得
得
AM=AFcos ∠FAM =2AEcos ∠EAB=2×8×![]() =
=![]() ,
,
∴MD=DA-AM=![]() .
.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】为了打造书香城市,截止2019年3月洛阳市有17家河洛书苑书房对社会免费开放.某书房为了解读者阅读的情况,随机调查了部分读者在一周内借阅图书的次数,并制成如图不完整的统计图表.
读者借阅图书的次数统计表
借阅图书的次数 | 1次 | 2次 | 3次 | 4次 | 5次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)这组数据的众数为 ,中位数为 ;
(3)请计算扇形统计图中的“4次”所对应的圆心角的度数;
(4)据统计该书房一周共有2000位不同的读者,根据以上调查结果,请你计算出一周内借阅图书“4次及以上”的读者人数.