题目内容
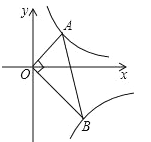
【题目】已知点A、B分别在反比例函数![]() (x>0),
(x>0),![]() (x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
(x>0)的图象上,且∠AOB=90°,则∠B=30°,则k的取值为( )
A. ![]() B.
B. ![]() C. ﹣2 D. ﹣3
C. ﹣2 D. ﹣3
【答案】D
【解析】
过A作AC垂直于y轴,过B作BD垂直于y轴,易证△AOC∽△OBD,利用反比例函数k的几何意义求出两三角形的面积,得出面积比,在直角三角形AOB中,利用锐角三角函数定义即可求出tan∠B的值,即OA与OB的比值,利用面积比等于相似比的平方,即可求出k值.
过A作AC⊥y轴,过B作BD⊥y轴,可得:∠ACO=∠BDO=90°,∴∠AOC+∠OAC=90°.
∵OA⊥OB,∴∠AOC+∠BOD=90°,∴∠OAC=∠BOD.
∵∠ACO=∠ODB=90°,∴△AOC∽△OBD.
∵点A、B分别在反比例函数y![]() (x>0),y
(x>0),y![]() (x>0)的图象上,∴S△AOC
(x>0)的图象上,∴S△AOC![]() ,S△OBD=|
,S△OBD=|![]() |,∴S△AOC:S△OBD=1:|k|,∴(
|,∴S△AOC:S△OBD=1:|k|,∴(![]() )2=1:|k|.在Rt△AOB中,tanB
)2=1:|k|.在Rt△AOB中,tanB![]() ,∴1:|k|=1:3,∴|k|=3.
,∴1:|k|=1:3,∴|k|=3.
∵y![]() (x>0)的图象在第四象限,∴k=﹣3.
(x>0)的图象在第四象限,∴k=﹣3.
故选D.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目