题目内容
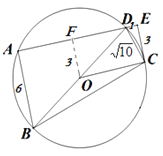
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,过C作CE⊥AD垂足为E,且∠EDC=∠BDC.
(1)求证:CE是⊙O的切线;
(2)若DE+CE=4,AB=6,求BD的值.

【答案】(1)详见解析;(2)BD=10.
【解析】试题分析:(1)根据已知条件易证∠OCE=90°,即可判定CE是⊙O的切线;(2)如图,过点O作OF⊥AE,垂足为F,即可得四边形OFEC为矩形,先求得OF的长,即可得CE的长,在Rt△EDC中,根据勾股定理可求得CD的长,再判定△EDC∽△CDB,根据相似三角形的性质即可求得BD的长.
试题解析:
(1)∵OC=OD,
∴∠ODC=∠OCD;
∵CE⊥AD,
∴∠ECD+∠CDE=90°,
∵∠EDC=∠BDC,
∴∠ECD+∠OCD=90°,
∴∠OCE=90°,
∴CE是⊙O的切线;
(2)如图,过点O作OF⊥AE,垂足为F,即可得四边形OFEC为矩形,
∵∠BAD=90°,
∴BD为直径,
∴∠BCD=90°,
∵OF⊥AE,
∴AF=DF,
∵OB=OD,AB=6,
∴OF=3.
∵四边形OFEC为矩形,
∴EC=OF=3,
∵DE+CE=4,
∴ED=1.
在Rt△EDC中,根据勾股定理可求得CD=![]() ,
,
∵∠DEC=∠BCD=90°,∠EDC=∠BDC
∴△EDC∽△CDB,
∴![]() ,
,
∴![]() ,
,
解得BD=10.

练习册系列答案
相关题目