题目内容
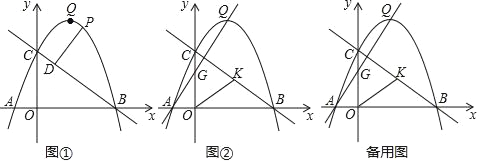
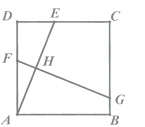
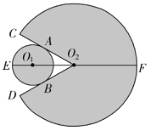
【题目】某玩具由一个圆形区域和一个扇形区域组成，如图，在⊙O1和扇形O2CD中，⊙O1与O2C、O2D分别切于点A、B，已知∠CO2D＝60°，E、F是直线O1O2与⊙O1、扇形O2CD的两个交点，且EF＝24cm，设⊙O1的半径为xcm，
（1）用含x的代数式表示扇形O2CD的半径；
（2）若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2，当⊙O1的半径为多少时，该玩具的制作成本最小？
【答案】（1）扇形O2CD的半径为（24-3x）cm；（2）当⊙O1的半径为4cm时，该玩具的制作成本最小．
【解析】
（1）连接O1A．利用切线的性质知∠AO2O1=
∠CO2D=30°；然后在Rt△O1AO2中利用“30°角所对的直角边是斜边的一半”求得O1O2=2xcm；最后由图形中线段间的和差关系求得扇形O2CD的半径FO2为：EF-EO1-O1O2=（24-3x）cm；
（2）设该玩具的制作成本为y元，则根据圆形的面积公式和扇形的面积公式列出y与x间的函数关系，然后利用二次函数的最值即可求得结果．
解：（1）连接O1A．
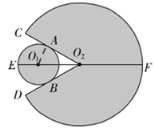
∵⊙O1与O2C、O2D分别切一点A、B，
∴O1A⊥O2C，O2E平分∠CO2D，
∴∠AO2O1=∠CO2D=30°，
∴在Rt△O1AO2中，O1O2=2AO1=2x cm．
∴FO2=EF-EO1-O1O2=（24-3x）cm，
即扇形O2CD的半径为（24-3x）cm．
（2）设该玩具的制作成本为y元，则
y=0.45πx2+0.06×
=0.9πx2-7.2πx+28.8π=0.9π（x-4）2+14.4π，
所以当x=4时，y的值最小．
答：当⊙O1的半径为4cm时，该玩具的制作成本最小．
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛，试卷题目共10题，每题10分．现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100．
整理数据：
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据：
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题：
（1）请直接写出表格中
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由；
（3）为了让学生重视安全知识的学习，学校将给竞赛成绩满分的同学颁发奖状，该校七年级新生共570人，试估计需要准备多少张奖状？
