Question

【题目】在和中，，，，点，，分别是，，的中点，连接，．

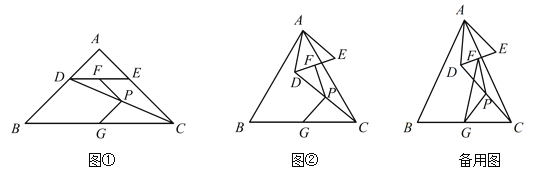
（1）如图①，，点在上，则 ；

（2）如图②，，点不在上，判断的度数，并证明你的结论；

（3）连接，若，，固定，将绕点旋转，当的长最大时，的长为 （用含的式子表示）．

Answer 1

【答案】（1）；（2），证明见解析；（3）

【解析】

（1）由AB=AC、AD=AE，得BD=CE，再根据G、P、F分别是BC、CD、DE的中点，可得出PG∥BD，PF∥CE．则∠GPF=180°—=90°；

（2）连接BD，连接CE，由已知可证明△ABD≌△ACE，则∠ABD=∠ACE．因为G、P、F分别是BC、CD、DE的中点，则PG∥BD，PF∥CE．进而得出∠GPF=180°—=120°；

（3）当D在BA的延长线上时，CE=BD最长，此时BD=AB+AD=5+2=7，再由三角形中位线定理即可算出PG=3.5，在Rt△GPH中，由三角函数的定义即可求出GH，进一步求出FG．

解：（1）∵AB=AC、AD=AE，

∴BD=CE，

∵G、P、F分别是BC、CD、DE的中点，

∴PG∥BD，PF∥CE．

∴∠ADC=∠DPG，∠DPF=∠ACD，

∴∠GPF=∠DPF+∠DPG=∠ADC+∠ACD=180°-∠BAC==90°，

即∠GPF=90°；

（2）∠FPG=120°，证明如下：

如图，连接BD，连接CE．如图②，

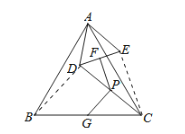
∵∠BAC=∠DAE，

∴∠BAD=∠CAE，

在△ABD和△ACE中，

，

∴△ABD≌△ACE（SAS），

∴∠ABD=∠ACE，

∵G、P、F分别是BC、CD、DE的中点，

∴PG∥BD，PF∥CE，

∴∠PGC=∠CBD，

∠DPF=∠DCE=∠DCA+∠ACE=∠DCA+∠ABD，

∠DPG=∠PGC+∠BCD=∠CBD+∠BCD，

∴∠GPF=∠DPF+∠DPG=∠DCA+∠ABD+∠CBD+∠BCD=180°—∠BAC=180°—=120°，

即∠GPF=120°；

（3）如图，连结BD，CE，过P作PH⊥FG于H，

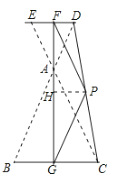
由（2）可知，△ABD≌△ACE，

∴BD=CE，且，

当D在BA的延长线上时，CE最长，即BD最长，此时BD=AB+AD=5+2=7，

∴PG=3.5，

∵PF=PG，PH⊥FG，

∴，FG=2HG，

∴，

故答案为：．