题目内容
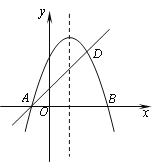
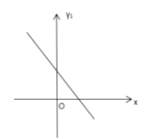
【题目】在平面直角坐标系中,函数y1=ax+b(a、b为常数,且ab≠0)的图象如图所示,y2=bx+a,设y=y1·y2.
(1)当b=-2a时,
①若点(1,4)在函数y的图象上,求函数y的表达式;
②若点(x1,p)和(x2,q)在函数y的图象上,且![]() ,比较p,q的大小;
,比较p,q的大小;
(2)若函数y的图象与x轴交于(m,0)和(n,0)两点,求证:m=![]() .
.
【答案】(1) ①y=(-2x+4)(4x-2);②p>q;(2)见解析.
【解析】
(1)①由题意可得y=(ax+b)(bx+a),把b=-2a与点(1,4)分别代入求得a的值,即可得到答案;
②令(ax-2a)(-2ax+a)=0,求得x的两个值,进而得到二次函数图象的对称轴为直线x=![]() ,再根据抛物线的性质即可判断p,q的大小关系;
,再根据抛物线的性质即可判断p,q的大小关系;
(2)令(ax+b)(bx+a)=0,解得x1=-![]() ,x2=-
,x2=-![]() ,即mn=1,整理即可得解.
,即mn=1,整理即可得解.
解:(1)y=(ax+b)(bx+a),
当b=-2a时,y=(ax-2a)(-2ax+a)
①把(1,4)代入,得,a2=4
由题意可知,a<0,则a=-2,
∴y=(-2x+4)(4x-2);
②令(ax-2a)(-2ax+a)=0,
得x1=2,x2=![]() ,
,
∴二次函数y的对称轴为直线x=![]() ,
,
∵![]() ,
,
∴点(x1,p)离对称轴较近,且抛物线y开口向下
所以p>q,
(3)令(ax+b)(bx+a)=0,
得,x1=-![]() ,x2=-
,x2=-![]() ,
,
∴mn=1,
∴m=![]() .
.

练习册系列答案
相关题目