ЬтФПФкШн
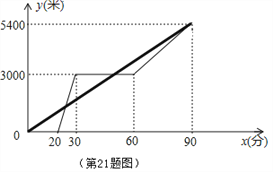
ЁОЬтФПЁПФГЫЎЙћХњЗЂЩЬЯњЪлУПЯфНјМлЮЊ40дЊЕФЦЛЙћЃЌЮяМлВПУХЙцЖЈУПЯфЪлМлВЛЕУИпгк55дЊЃЌЪаГЁЕїВщЗЂЯжЃЌШєУПЯфвд50дЊЕФМлИёЯњЪлЃЌЦНОљУПЬьЯњЪл90ЯфЃЌМлИёУПЬсИп1дЊЃЌЦНОљУПЬьЩйЯњЪл3ЯфЃЎ
ЃЈ1ЃЉЧѓЦНОљУПЬьЯњЪлСП![]() ЯфгыЯњЪлМл
ЯфгыЯњЪлМл![]() дЊ/ЯфжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
дЊ/ЯфжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ2ЃЉЧѓИУХњЗЂЩЬЦНОљУПЬьЕФЯњЪлРћШѓwЃЈдЊЃЉгыЯњЪлМл![]() ЃЈдЊ/ЯфЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈдЊ/ЯфЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉЕБУПЯфЦЛЙћЕФЯњЪлМлЮЊЖрЩйдЊЪБЃЌПЩвдЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉгЩЬтвтЕУЃК
y=90-3ЃЈx-50ЃЉ
ЛЏМђЕУЃКy=-3x+240ЃЛ
ЃЈ2ЃЉгЩЬтвтЕУЃК
w=ЃЈx-40ЃЉЃЈ-3x+240ЃЉ
=-3x2+360x-9600ЃЛ
ЃЈ3ЃЉw=-3x2+360x-9600
Ёпa=-3ЃМ0ЃЌ
ЁрХзЮяЯпПЊПкЯђЯТЃЎ
ЕБ![]() ЪБЃЌwгазюДѓжЕЃЎ
ЪБЃЌwгазюДѓжЕЃЎ
гжxЃМ60ЃЌwЫцxЕФдіДѓЖјдіДѓЃЎ
ЁрЕБx=55дЊЪБЃЌwЕФзюДѓжЕЮЊ1125дЊЃЎ
ЁрЕБУПЯфЦЛЙћЕФЯњЪлМлЮЊ55дЊЪБЃЌПЩвдЛёЕУ1125дЊЕФзюДѓРћШѓЃЎ
ЁОНтЮіЁП
ЪдЬтБОЬтЪЧЭЈЙ§ЙЙНЈКЏЪ§ФЃаЭНтД№ЯњЪлРћШѓЕФЮЪЬтЃЎвРОнЬтвтвзЕУГіЦНОљУПЬьЯњЪлСПЃЈyЃЉгыЯњЪлМлxЃЈдЊ/ЯфЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊy=90Љ3ЃЈxЉ50ЃЉЃЌШЛКѓИљОнЯњЪлРћШѓ=ЯњЪлСПЁСЃЈЪлМлЉНјМлЃЉЃЌСаГіЦНОљУПЬьЕФЯњЪлРћШѓwЃЈдЊЃЉгыЯњЪлМлxЃЈдЊ/ЯфЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌдйвРОнКЏЪ§ЕФдіМѕадЧѓЕУзюДѓРћШѓЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЕУЃК
y=90Љ3ЃЈxЉ50ЃЉ
ЛЏМђЕУЃКy=Љ3x+240ЃЛЃЈ3ЗжЃЉ
ЃЈ2ЃЉгЩЬтвтЕУЃК
w=ЃЈxЉ40ЃЉy
ЃЈxЉ40ЃЉЃЈЉ3x+240ЃЉ
=Љ3x2+360xЉ9600ЃЛЃЈ3ЗжЃЉ
ЃЈ3ЃЉw=Љ3x2+360xЉ9600
Ёпa=Љ3ЃМ0ЃЌ
ЁрХзЮяЯпПЊПкЯђЯТЃЎ
ЕБ![]() ЪБЃЌwгазюДѓжЕЃЎ
ЪБЃЌwгазюДѓжЕЃЎ
гжxЃМ60ЃЌwЫцxЕФдіДѓЖјдіДѓЃЎ
ЁрЕБx=55дЊЪБЃЌwЕФзюДѓжЕЮЊ1125дЊЃЎ
ЁрЕБУПЯфЦЛЙћЕФЯњЪлМлЮЊ55дЊЪБЃЌПЩвдЛёЕУ1125дЊЕФзюДѓРћШѓЃЎЃЈ4ЗжЃЉ

 УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ
УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ