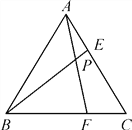
题目内容
【题目】已知Rt△ABC,∠BAC=90°,点D是BC中点,AD=AC,BC=4![]() ,过A,D两点作⊙O,交AB于点E,
,过A,D两点作⊙O,交AB于点E,
(1)求弦AD的长;
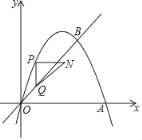
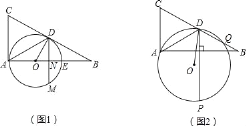
(2)如图1,当圆心O在AB上且点M是⊙O上一动点,连接DM交AB于点N,求当ON等于多少时,三点D、E、M组成的三角形是等腰三角形?
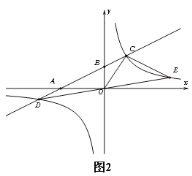
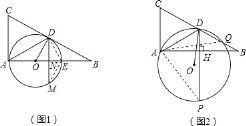
(3)如图2,当圆心O不在AB上且动圆⊙O与DB相交于点Q时,过D作DH⊥AB(垂足为H)并交⊙O于点P,问:当⊙O变动时DP﹣DQ的值变不变?若不变,请求出其值;若变化,请说明理由.
【答案】(1)![]()
(2)当ON等于1或![]() ﹣1时,三点D、E、M组成的三角形是等腰三角形
﹣1时,三点D、E、M组成的三角形是等腰三角形
(3)不变,理由见解析
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半即可得到AD的长;
(2)连DE、ME,易得当ED和EM为等腰三角形EDM的两腰,根据垂径定理得推论得OE⊥DM,易得到△ADC为等边三角形,得∠CAD=60°,则∠DAO=30°,∠DON=60°,然后根据含30°的直角三角形三边的关系得DN=![]() AD=
AD=![]() ,ON=
,ON=![]() DN=1;
DN=1;
当MD=ME,DE为底边,作DH⊥AE,由于AD=2![]() ,∠DAE=30°,得到DH=
,∠DAE=30°,得到DH=![]() ,∠DEA=60°,DE=2,于是OE=DE=2,OH=1,
,∠DEA=60°,DE=2,于是OE=DE=2,OH=1,
又∠M=∠DAE=30°,MD=ME,得到∠MDE=75°,则∠ADM=90°-75°=15°,可得到∠DNO=45°,根据等腰直角三角形的性质得到NH=DH=![]() ,则ON=
,则ON=![]() -1;
-1;
(3)连AP、AQ,DP⊥AB,得AC∥DP,则∠PDB=∠C=60°,再根据圆周角定理得∠PAQ=∠PDB,∠AQC=∠P,则∠PAQ=60°,∠CAQ=∠PAD,易证得△AQC≌△APD,得到
DP=CQ,则DP-DQ=CQ-DQ=CD,而△ADC为等边三角形,CD=AD=2![]() ,即可得到DP-DQ的值.
,即可得到DP-DQ的值.
解:(1)∵∠BAC=90°,点D是BC中点,BC=4![]() ,
,
∴AD=![]() BC=
BC=![]() ;
;
(2)连DE、ME,如图,∵DM>DE,
当ED和EM为等腰三角形EDM的两腰,
∴OE⊥DM,
又∵AD=AC,
∴△ADC为等边三角形,
∴∠CAD=60°,
∴∠DAO=30°,
∴∠DON=60°,
在Rt△ADN中,DN=![]() AD=
AD=![]() ,
,
在Rt△ODN中,ON=![]() DN=1,
DN=1,
∴当ON等于1时,三点D、E、M组成的三角形是等腰三角形;
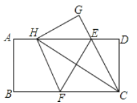
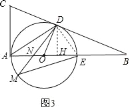
当MD=ME,DE为底边,如图3,作DH⊥AE,
∵AD=2![]() ,∠DAE=30°,
,∠DAE=30°,
∴DH=![]() ,∠DEA=60°,DE=2,
,∠DEA=60°,DE=2,
∴△ODE为等边三角形,
∴OE=DE=2,OH=1,
∵∠M=∠DAE=30°,
而MD=ME,
∴∠MDE=75°,
∴∠ADM=90°﹣75°=15°,
∴∠DNO=45°,
∴△NDH为等腰直角三角形,
∴NH=DH=![]() ,
,
∴ON=![]() ﹣1;
﹣1;
综上所述,当ON等于1或![]() ﹣1时,三点D、E、M组成的三角形是等腰三角形;
﹣1时,三点D、E、M组成的三角形是等腰三角形;
(3)当⊙O变动时DP﹣DQ的值不变,DP﹣DQ=2![]() .理由如下:
.理由如下:
连AP、AQ,如图2,
∵∠C=∠CAD=60°,
而DP⊥AB,
∴AC∥DP,
∴∠PDB=∠C=60°,
又∵∠PAQ=∠PDB,
∴∠PAQ=60°,
∴∠CAQ=∠PAD,
∵AC=AD,∠AQC=∠P,
∴△AQC≌△APD,
∴DP=CQ,
∴DP﹣DQ=CQ﹣DQ=CD=2![]() .
.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
有下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③x=3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
小明从中任意选取一个结论,则选中正确结论的概率为( )
A. 1B. ![]() C.
C. ![]() D.
D. ![]()