题目内容
【题目】如图所示,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1 , 与x轴的另一个交点为A1 . 
(1)当a=﹣1,b=1时,求抛物线n的解析式;
(2)四边形AC1A1C是什么特殊四边形,请写出结果并说明理由;
(3)若四边形AC1A1C为矩形,请求出a,b应满足的关系式.
【答案】
(1)
解:当a=﹣1,b=1时,抛物线m的解析式为:y=﹣x2+1.
令x=0,得:y=1.
∴C(0,1).
令y=0,得:x=±1.
∴A(﹣1,0),B(1,0),
∵C与C1关于点B中心对称,
∴抛物线n的解析式为:y=(x﹣2)2﹣1=x2﹣4x+3
(2)
解:四边形AC1A1C是平行四边形.
理由:连接AC,AC1,A1C1,
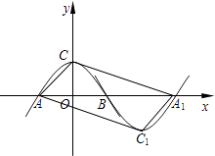
∵C与C1、A与A1都关于点B中心对称,
∴AB=BA1,BC=BC1,
∴四边形AC1A1C是平行四边形
(3)
解:令x=0,得:y=b.
∴C(0,b).
令y=0,得:ax2+b=0,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
要使平行四边形AC1A1C是矩形,必须满足AB=BC,
∴ ![]() ,
,
∴ ![]() ,
,
∴ab=﹣3.
∴a,b应满足关系式ab=﹣3.
【解析】(1)根据a=﹣1,b=1得出抛物线m的解析式,再利用C与C1关于点B中心对称,得出二次函数的顶点坐标,即可得出答案;(2)利用两组对边分别相等的四边形是平行四边形即可证明;(3)利用矩形性质得出要使平行四边形AC1A1C是矩形,必须满足AB=BC,即可求出.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.

练习册系列答案
相关题目