题目内容
【题目】如图,将△ABC沿角平分线BD所在直线翻折,顶点A恰好落在边BC的中点E处,AE=BD,那么tan∠ABD= . 
【答案】![]()
【解析】解:如图,作CM⊥AE交AE的延长线于M,作DN⊥AB于N,DF⊥BC于F,AE与BD交于点K,设DK=a. 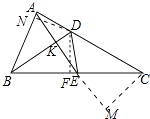
∵AB=BE=EC,
∴BC=2AB,
∵DB平分∠ABC,
∴DN=DF,
∵ ![]() =
=  =
= ![]() ,
,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∵DB⊥AM,CM⊥AM,
∴DK∥CM,
∴ ![]() =
= ![]() =
= ![]() ,∠KBE=∠MCE,
,∠KBE=∠MCE,
∴CM=3a,
在△BKE和△CME中,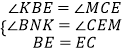 ,
,
∴△BKE≌△CME,
∴BK=CM=3a,
∴BD=AE=4a,
∴AK=KE=2a,
∴tan∠ABD= ![]() =
= ![]() =
= ![]() .
.
所以答案是 ![]() .
.
补充方法:取DC的中点P,连接EP,利用三角形的中位线,可以证明BK=3DK,根据AK= ![]() BD,
BD,
根据tan∠ABD= ![]() =
= ![]() .
.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
相关题目