题目内容
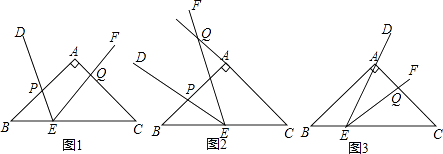
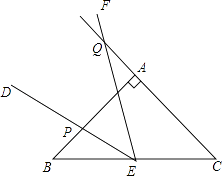
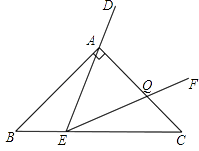
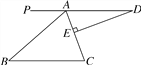
【题目】如图，AD∥BC，∠BAC＝70°，DE⊥AC于点E，∠D＝20°.
(1)求∠B的度数，并判断△ABC的形状；
(2)若延长线段DE恰好过点B，试说明DB是∠ABC的平分线．
【答案】（1）△ABC是等腰三角形，∠B＝40°；（2）见解析.
【解析】(1)、根据Rt△ADE的内角和得出∠DAC=70°，根据平行线的性质得出∠C=70°，从而根据有两个角相等的三角形是等腰三角形得出答案；(2)、根据等腰三角形底边上的三线合一定理得出DB为顶角的角平分线．
解：(1)∵DE⊥AC于点E，∠D＝20°，∴∠CAD＝70°， ∵AD∥BC，
∴∠C＝∠CAD＝70°， 又∵∠BAC＝70°，∴∠BAC＝∠C，∴AB＝BC，
∴△ABC是等腰三角形，∴∠B＝180°－∠BAC－∠C＝180°－70°－70°＝40°.
(2)∵延长线段DE恰好过点B，DE⊥AC，∴BD⊥AC，∵△ABC是等腰三角形，
∴DB是∠ABC的平分线．
练习册系列答案
名校课堂系列答案
相关题目
