题目内容
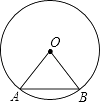
【题目】如图,四边形ABCD内接于圆O,点E在对角线AC上. 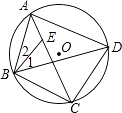
(1)若BC=DC,∠CBD=39°,求∠BCD的度数;
(2)若在AC上有一点E,且EC=BC=DC,求证:∠1=∠2.
【答案】
(1)解:∵BC=CD,
∴ ![]() =
= ![]() ,
,
∴∠BAC=∠DAC=∠CBD=39°,
∴∠BAD=78°,
∵四边形ABCD为圆内接四边形,
∴∠BCD=102°;
(2)解:∵BC=CD,
∴∠CBD=∠CDB,又∠BAC=∠BDC,
∴∠CBD=∠BAE,
∴∠CEB=∠BAE+∠2,
∵CB=CE,
∴∠CBE=∠CEB,
∴∠BAE+∠2=∠CBD+∠1,
∴∠1=∠2.
【解析】(1)根据BC=CD,得到 ![]() =
= ![]() ,求出∠BAD=78°,根据圆内接四边形的性质计算即可;(2)根据等腰三角形的性质和三角形的外角的性质解答即可.
,求出∠BAD=78°,根据圆内接四边形的性质计算即可;(2)根据等腰三角形的性质和三角形的外角的性质解答即可.
【考点精析】掌握等腰三角形的性质和圆周角定理是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目