Question

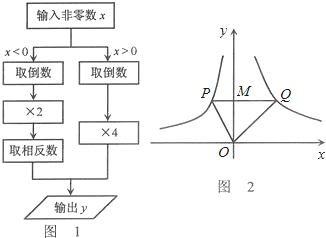
已知如图，点A（m，3）与点B（n，2）关于直线y=x对称，且都在反比例函数y=

k

x

的图象上，点D的坐标为（0，-2）．
（1）求反比例函数的解析式；
（2）若过B，D的直线与x轴交于点C，求sin∠DCO的值．

Answer 1

（1）∵A（m，3）与B（n，2）关于直线y=x对称，
∴m=2，n=3，
即A（2，3），B（3，2）．
于是由3=

k

2

，
∴k=6，
∴反比例函数的解析式为y=

6

x

；

（2）设直线的解析式为y=kx+b，
将B（3，2），D（0，-2）代入得：

2=3k+b -2=0•k+b

，
解得：

k= 4 3 b=-2

，
故直线BD的解析式为y=

4

3

x-2，
∴当y=0时，
∴x=1.5．
即C（1.5，0），
于是OC=1.5，DO=2，
在Rt△OCD中，DC=

1.52+22

=2.5，
∴sin∠DCO=

DO

DC

=

2

2.5

=

4

5

．
说明：过点B作BE⊥y轴于E，则BE=3，DE=4，从而BD=5，sin∠DCO=sin∠DBE=

4

5

．