题目内容
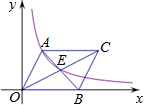
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=
(x>0)的图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点
①求反比例函数解析式;
②通过计算,说明一次函数y=kx+3-3k(k≠0)的图象一定过点C;
③对于一次函数y=kx+3-kx(k≠0)当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写过程)

| m |
| x |
①求反比例函数解析式;
②通过计算,说明一次函数y=kx+3-3k(k≠0)的图象一定过点C;
③对于一次函数y=kx+3-kx(k≠0)当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写过程)

(1)∵四边形ABCD是平行四边形,
∴AD=BC,
∵B(3,1),C(3,3),
∴BC⊥x轴,AD=BC=2,
而A点坐标为(1,0),
∴点D的坐标为(1,2).
∵反比例函数y=
(x>0)的函数图象经过点D(1,2),
∴2=
,
∴m=2,
∴反比例函数的解析式为y=
;
(2)当x=3时,y=kx+3-3k=3k+3-3k=3,
∴一次函数y=kx+3-3k(k≠0)的图象一定过点C;
(3)设点P的横坐标为a,
∵一次函数y=kx+3-3k(k≠0)过C点,并且y随x的增大而增大时,
∴k>0,P点的纵坐标要小于3,横坐标要小于3,
当纵坐标小于3时,∵y=
,∴
<3,解得:a>
,
则a的范围为
<a<3.
∴AD=BC,
∵B(3,1),C(3,3),
∴BC⊥x轴,AD=BC=2,
而A点坐标为(1,0),
∴点D的坐标为(1,2).
∵反比例函数y=
| m |
| x |
∴2=
| m |
| 1 |
∴m=2,
∴反比例函数的解析式为y=
| 2 |
| x |
(2)当x=3时,y=kx+3-3k=3k+3-3k=3,
∴一次函数y=kx+3-3k(k≠0)的图象一定过点C;
(3)设点P的横坐标为a,
∵一次函数y=kx+3-3k(k≠0)过C点,并且y随x的增大而增大时,
∴k>0,P点的纵坐标要小于3,横坐标要小于3,
当纵坐标小于3时,∵y=
| 2 |
| x |
| 2 |
| a |
| 2 |
| 3 |
则a的范围为
| 2 |
| 3 |

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 为(1,1).
为(1,1). (1)求一次函数解析式;
(1)求一次函数解析式;