Question

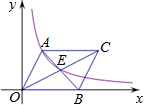
如图，在直角坐标系中，矩形OABC的顶点A、B在双曲线y=

k

x

（x＞0）上，BC与x轴交于点D．若点A的坐标为（1，2），则点B的坐标为（　　）

A．（3， 2 3 ）

B．（4， 1 2 ）

C．（ 9 2 ， 4 9 ）

D．（5， 2 5 ）

Answer 1

∵矩形OABC的顶点A、B在双曲线y=

k

x

（ x＞0）上，点A的坐标为（1，2），
∴2=

k

1

，
解得：k=2，
∴双曲线的解析式为：y=

2

x

，直线OA的解析式为：y=2x，
∵OA⊥AB，
∴设直线AB的解析式为：y=-

1

2

x+b，
∴2=-

1

2

×1+b，
解得：b=

5

2

，
∴直线AB的解析式为：y=-

1

2

x+

5

2

，
将直线AB与反比例函数联立得出：

y= 2 x y=- 1 2 x+ 5 2

，
解得：

x=4 y= 1 2

或

x=1 y=2

，
∴点B（4，

1

2

）．
故选B．